题目内容
 如图,梯形ABCD中,AB∥CD,且AB=2CD,对角线AC、DB相交于点O.若
如图,梯形ABCD中,AB∥CD,且AB=2CD,对角线AC、DB相交于点O.若| AD |
| a |
| AB |
| b |
| OC |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:先证明△DOC∽△BOA,然后根据AB=2CD得到AO与AD的比例关系,最后转化成用基底表示即可.
解答:
解:∵AB∥CD,AB=2CD,
∴△DOC∽△BOA且AO=2OC,
则
=2
=
,∴
=
,而
=
+
=
+
=
+
,
∴
=
=
(
+
)=
+
,
故选B.
∴△DOC∽△BOA且AO=2OC,
则
| AO |
| OC |
| 2 |
| 3 |
| AC |
| OC |
| 1 |
| 3 |
| AC |
| AC |
| AD |
| DC |
| AD |
| 1 |
| 2 |
| AB |
| a |
| 1 |
| 2 |
| b |
∴
| OC |
| 1 |
| 3 |
| AC |
| 1 |
| 3 |
| a |
| 1 |
| 2 |
| b |
| 1 |
| 3 |
| a |
| 1 |
| 6 |
| b |
故选B.
点评:本题主要考查了向量加减混合运算及其几何意义,解题的关键是弄清AO与AD的比例关系,属于基础题.

练习册系列答案
相关题目
 将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的左视图为( )
将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的左视图为( )A、 |
B、 |
C、 |
D、 |
已知a>b,c>d,则下列不等式成立的是( )
| A、b+d<a+c | ||||
| B、ac>bd | ||||
C、
| ||||
| D、a-c>b-d |
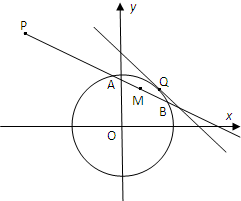 过点P(-4,4)作直线l与圆O:x2+y2=4相交于A、B两点.
过点P(-4,4)作直线l与圆O:x2+y2=4相交于A、B两点.