题目内容
13.设x∈R,若“|x-a|<1(a∈R)”是“x2+x-2>0”的充分不必要条件,则a的取值范围是( )| A. | (-∞,-3]∪[2,+∞) | B. | (-∞,-3)∪(2,+∞) | C. | (-3,2) | D. | [-3,2] |
分析 由|x-a|<1(a∈R),解得x.由x2+x-2>0,解得x.又“|x-a|<1(a∈R)”是“x2+x-2>0”的充分不必要条件,可得1≤a-1,或a+1≤-2.即可得出.
解答 解:由|x-a|<1(a∈R),解得:a-1<x<a+1.
由x2+x-2>0,解得x>1或x<-2.
又“|x-a|<1(a∈R)”是“x2+x-2>0”的充分不必要条件,
∴1≤a-1,或a+1≤-2.
∴a≥2,或a≤-3.
故选:A.
点评 本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
1.一已知等差数列{an}中,其前n项和为Sn,若a3+a4+a5=42,则S7=( )
| A. | 98 | B. | 49 | C. | 14 | D. | 147 |
8.设集合A={x|$\frac{x-2}{x+3}$≤0},B={x|-4≤x≤1},则A∩B=( )
| A. | [-3,1] | B. | [-4,2] | C. | [-2,1] | D. | (-3,1] |
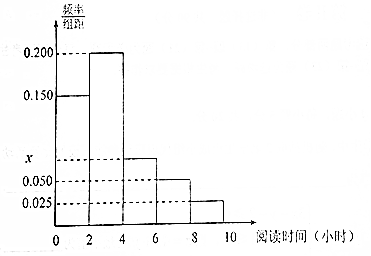 某学校为了了解本校高一学生每周课外阅读时间(单位:小时)的情况,按10%的比例对该校高一600名学生进行抽样统计,将样本数据分为5组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10),并将所得数据绘制成如图所示的频率分布直方图:
某学校为了了解本校高一学生每周课外阅读时间(单位:小时)的情况,按10%的比例对该校高一600名学生进行抽样统计,将样本数据分为5组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10),并将所得数据绘制成如图所示的频率分布直方图: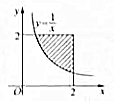 在平面直角坐标系内任取一个点P(x,y)满足$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤2}\end{array}\right.$,则点P落在曲线y=$\frac{1}{x}$与直线x=2,y=2围成的阴影区域(如图所示)内的概率为$\frac{3-ln4}{4}$.
在平面直角坐标系内任取一个点P(x,y)满足$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤2}\end{array}\right.$,则点P落在曲线y=$\frac{1}{x}$与直线x=2,y=2围成的阴影区域(如图所示)内的概率为$\frac{3-ln4}{4}$.


