题目内容
8．设集合A={x|$\frac{x-2}{x+3}$≤0}，B={x|-4≤x≤1}，则A∩B=（ ）| A． | [-3，1] | B． | [-4，2] | C． | [-2，1] | D． | （-3，1] |
分析 先分别求出集合A和B，由此利用交集定义能求出A∩B．
解答 解：∵集合A={x|$\frac{x-2}{x+3}$≤0}={x|-3＜x≤2}，
B={x|-4≤x≤1}，
∴A∩B={x|-3＜x≤1}=（-3，1]．
故选：D．
点评 本题考查交集的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．
练习册系列答案
快乐5加2金卷系列答案
相关题目
19．
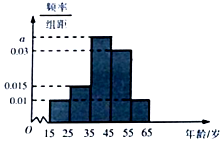2017年郴州市两会召开前夕，某网站推出两会热点大型调查，调查数据表明，民生问题是百姓最为关心的热点，参与调查者中关注此问题的约占80%，现从参与者中随机选出200人，并将这200人按年龄分组：第1组[15，25），第2组[25，35），第3组[35，45），第4组[45，55），第5组[55，65），得到的频率分布直方图如图所示：
（Ⅰ）求出频率分布直方图中a的值，并求出这200人的平均年龄；
（Ⅱ）现在要从年龄较小的第1组和第2组中用分层抽样的方法抽取5人，再从这5人中随机抽取2人赠送礼品，求抽取的2人中至少有人年龄在第1组的概率；
（Ⅲ）把年龄在第1，2，3组的居民称为青少年组，年龄在第4，5组的居民称为中老年组，若选出的200人中不关注民生问题的人中老年人有10人，根据以上数据，完成以下列联表，并判断是否可以在犯错误概率不超过1%的前提下，认为关注民生问题与年龄有关？
附：
${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
2017年郴州市两会召开前夕，某网站推出两会热点大型调查，调查数据表明，民生问题是百姓最为关心的热点，参与调查者中关注此问题的约占80%，现从参与者中随机选出200人，并将这200人按年龄分组：第1组[15，25），第2组[25，35），第3组[35，45），第4组[45，55），第5组[55，65），得到的频率分布直方图如图所示：（Ⅰ）求出频率分布直方图中a的值，并求出这200人的平均年龄；
（Ⅱ）现在要从年龄较小的第1组和第2组中用分层抽样的方法抽取5人，再从这5人中随机抽取2人赠送礼品，求抽取的2人中至少有人年龄在第1组的概率；
（Ⅲ）把年龄在第1，2，3组的居民称为青少年组，年龄在第4，5组的居民称为中老年组，若选出的200人中不关注民生问题的人中老年人有10人，根据以上数据，完成以下列联表，并判断是否可以在犯错误概率不超过1%的前提下，认为关注民生问题与年龄有关？
| 关注民生 | 不关注民生 | 合计 | |
| 青少年组 | 90 | 30 | 120 |
| 中老年组 | 70 | 10 | 80 |
| 合计 | 160 | 40 | 200 |
| p（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
3．
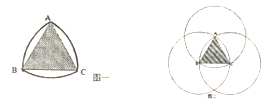如图一所示，由弧AB，弧AC，弧BC所组成的图形叫做勒洛三角形，它由德国机械工程专家、机械运动学家勒洛首先发现的，它的构成如图二所示，以正三角形ABCd的每个顶点为圆心，以边长为半径，在另两个顶点间作一段弧，由三段弧所围成的曲边三角形即为勒洛三角形，有一个如图一所示的靶子，某人向靶子射出一箭，若此箭一定能射中靶子且射中靶子中的任意一点是等可能的，则此箭恰好射中三角形ABC内部（即阴影部分）的概率为（ ）
如图一所示，由弧AB，弧AC，弧BC所组成的图形叫做勒洛三角形，它由德国机械工程专家、机械运动学家勒洛首先发现的，它的构成如图二所示，以正三角形ABCd的每个顶点为圆心，以边长为半径，在另两个顶点间作一段弧，由三段弧所围成的曲边三角形即为勒洛三角形，有一个如图一所示的靶子，某人向靶子射出一箭，若此箭一定能射中靶子且射中靶子中的任意一点是等可能的，则此箭恰好射中三角形ABC内部（即阴影部分）的概率为（ ）| A． | $\frac{\sqrt{3}}{2π-\sqrt{3}}$ | B． | $\frac{\sqrt{3}}{2（π-\sqrt{3}}）$ | C． | $\frac{2π-3\sqrt{3}}{2（π-\sqrt{3}）}$ | D． | $\frac{2π-2\sqrt{3}}{2π-\sqrt{3}}$ |
13．设x∈R，若“|x-a|＜1（a∈R）”是“x2+x-2＞0”的充分不必要条件，则a的取值范围是（ ）
| A． | （-∞，-3]∪[2，+∞） | B． | （-∞，-3）∪（2，+∞） | C． | （-3，2） | D． | [-3，2] |
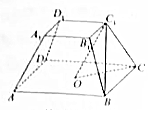如图，正四棱台ABCD-A1B1C1D1的高为2，下底面中心为O，上、下底面边长分别为2和4．
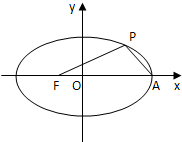如图，焦点在x轴上的椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$，F、A分别是椭圆的一个焦点和顶点，P是椭圆上任意一点，则$\overrightarrow{PF}$•$\overrightarrow{PA}$的最大值为4．
16．已知圆M过定点（0，1）且圆心M在抛物线x2=2y上运动，若x轴截圆M所得的弦为|PQ|，则弦长|PQ|等于（ ）
| A． | 2 | B． | 3 | ||
| C． | 4 | D． | 与点位置有关的值 |