题目内容
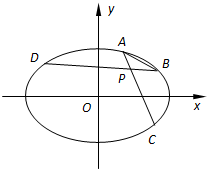 如图所示,在平面直角坐标系xOy中,设椭圆E:
如图所示,在平面直角坐标系xOy中,设椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| AP |
| PC |
| BP |
| PD |
| 5 |
| 7 |
(1)求椭圆E的离心率;
(2)求a与b的值;
(3)当λ变化时,kAB是否为定值?若是,请求出此定值;若不是,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由b=
a,得到
a2=c2,由此能求出离心率.
(2)求出A(
,
),代入到椭圆方程中,能求出a=2,b=
.
(3)法一:设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),由
=λ
,得
,推导出3x1+4y1=3x2+4y2,由此能求出kAB=-
为定值.
(3)法二:设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),由点差法求出3(x1+x2)+4(y1+y2)kAB=0,3(x3+x4)+4(y3+y4)kCD=0,由此推导出kAB=-
为定值.
| ||
| 2 |
| 1 |
| 4 |
(2)求出A(
| 12-5a |
| 7 |
| 12 |
| 7 |
| 3 |
(3)法一:设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),由
| AP |
| PC |
|
| 3 |
| 4 |
(3)法二:设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),由点差法求出3(x1+x2)+4(y1+y2)kAB=0,3(x3+x4)+4(y3+y4)kCD=0,由此推导出kAB=-
| 3 |
| 4 |
解答:
(本小题满分16分)
解:(1)因为b=
a,
所以b2=
a2,整理得a2-c2=
a2,即
a2=c2,
所以离心率e=
=
.…(4分)
(2)因为C(a,0),λ=
,
所以由
=λ
,得A(
,
),…(7分)
将它代入到椭圆方程中,
得
+
=1,解得a=2,
所以a=2,b=
.…(10分)
(3)解法一:设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
由
=λ
,得
,…(12分)
又椭圆的方程为
+
=1,
所以由
+
=1,
+
=1,
得3x12+4y12=12①,且3(
+1)2+4(
+1)2=12②,
由②得,
[3(1-x1)2+4(1-y1)2]+
[3(1-x1)+4(1-y1)]=5,
即
[(3x12+4y12)+7-2(3x1+4y1)]+
[7-(3x1+4y1)]=5,
结合①,得3x1+4y1=
,…(14分)
同理,有3x2+4y2=
,
所以3x1+4y1=3x2+4y2,
从而
=-
,即kAB=-
为定值.…(16分)
(3)解法二:设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
由
=λ
,得
,
同理
,…(12分)
将A,B坐标代入椭圆方程得
,
两式相减得3(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0,
即3(x1+x2)+4(y1+y2)kAB=0,…(14分)
同理,3(x3+x4)+4(y3+y4)kCD=0,
而kAB=kCD,所以3(x3+x4)+4(y3+y4)kAB=0,
所以3λ(x3+x4)+4λ(y3+y4)kAB=0,
所以3(x1+λx3+x2+λx4)+4(y1+λy3+y2+λy4)kAB=0,
即6(1+λ)+8(1+λ)k=0,所以kAB=-
为定值.…(16分)
解:(1)因为b=
| ||
| 2 |
所以b2=
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
所以离心率e=
| c |
| a |
| 1 |
| 2 |
(2)因为C(a,0),λ=
| 5 |
| 7 |
所以由
| AP |
| PC |
| 12-5a |
| 7 |
| 12 |
| 7 |
将它代入到椭圆方程中,
得
| (12-5a)2 |
| 49a2 |
| 122 | ||
49×
|
所以a=2,b=
| 3 |
(3)解法一:设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
由
| AP |
| PC |
|
又椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
所以由
| x12 |
| 4 |
| y12 |
| 3 |
| x32 |
| 4 |
| y32 |
| 3 |
得3x12+4y12=12①,且3(
| 1-x1 |
| λ |
| 1-y1 |
| λ |
由②得,
| 1 |
| λ2 |
| 2 |
| λ2 |
即
| 1 |
| λ2 |
| 2 |
| λ2 |
结合①,得3x1+4y1=
| 19+14λ-5λ2 |
| 2λ+2 |
同理,有3x2+4y2=
| 19+14λ-5λ2 |
| 2λ+2 |
所以3x1+4y1=3x2+4y2,
从而
| y1-y2 |
| x1-x2 |
| 3 |
| 4 |
| 3 |
| 4 |
(3)解法二:设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
由
| AP |
| PC |
|
同理
|
将A,B坐标代入椭圆方程得
|
两式相减得3(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0,
即3(x1+x2)+4(y1+y2)kAB=0,…(14分)
同理,3(x3+x4)+4(y3+y4)kCD=0,
而kAB=kCD,所以3(x3+x4)+4(y3+y4)kAB=0,
所以3λ(x3+x4)+4λ(y3+y4)kAB=0,
所以3(x1+λx3+x2+λx4)+4(y1+λy3+y2+λy4)kAB=0,
即6(1+λ)+8(1+λ)k=0,所以kAB=-
| 3 |
| 4 |
点评:本题考查椭圆的离心率的求法,考查椭圆方程的求法,考查直线的斜率是否为定值的判断与求法,解题时要认真审题,注意点差法的合理运用.

练习册系列答案
相关题目
已知集合A={2,3,4},B={3,4,5},则A∩B=( )
| A、{3} |
| B、{3,4} |
| C、{2,3,4} |
| D、{2,3,4,5} |
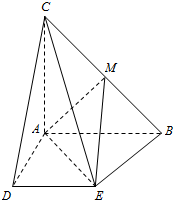 在△ABC中,AB=AC,∠CAB=90°,且
在△ABC中,AB=AC,∠CAB=90°,且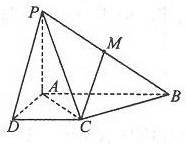 已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,M为PB中点.
已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,M为PB中点.