题目内容
已知函数f(x)=2cosx•sin(x+
)-
sin2x+sinx•cosx.
(1)求函数f(x)的单调递减区间;
(2)将函数f(x)的图象按向量
=(m,0)平移后得到g(x)的图象,求使函数g(x)为偶函数的m的最小正值.
| π |
| 3 |
| 3 |
(1)求函数f(x)的单调递减区间;
(2)将函数f(x)的图象按向量
| a |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:利用倍角公式及和差公式把f(x)化成正弦型函数的标准形式,(1)根据正弦函数的单调区间求函数f(x)的单调区间;(2)由图象平移求出g(x)的解析式,由g(x)为偶函数得到m关于k的表达式,进而求出m的最小值.
解答:
解:f(x)=2cosx•sin(x+
)-
sin2x+sinx•cosx
=2cosx(
sinx+
cosx)-
(1-cos2x)+
sin2x
=
sin2x+
(1+cos2x)-
+
cos2x+
sin2x
=sin2x+
cos2x
=2sin(2x+
);
(1)由
+2kπ≤2x+
≤
+2kπ(k∈Z)
得:
+kπ≤x≤
+kπ(k∈Z)
所以函数f(x)的单调递减区间为[
+kπ,
+kπ](k∈Z).
(2)函数f(x)的图象按向量
=(m,0)平移后得到
g(x)=2sin[2(x-m)+
]=2sin(2x-2m+
)
要使g(x)为偶函数,须-2m+
=
+kπ(k∈Z)
∴m=-
-
(k∈Z)
当k=-1,m取最小值
所以使函数g(x)为偶函数的m的最小正值为
.
| π |
| 3 |
| 3 |
=2cosx(
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
=sin2x+
| 3 |
=2sin(2x+
| π |
| 3 |
(1)由
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
得:
| π |
| 12 |
| 7π |
| 12 |
所以函数f(x)的单调递减区间为[
| π |
| 12 |
| 7π |
| 12 |
(2)函数f(x)的图象按向量
| a |
g(x)=2sin[2(x-m)+
| π |
| 3 |
| π |
| 3 |
要使g(x)为偶函数,须-2m+
| π |
| 3 |
| π |
| 2 |
∴m=-
| π |
| 12 |
| kπ |
| 2 |
当k=-1,m取最小值
| 5π |
| 12 |
所以使函数g(x)为偶函数的m的最小正值为
| 5π |
| 12 |
点评:本题考查了三角变换及三角函数的图象与性质,解决本题的关键是把函数f(x)化成正弦型函数的标准形式.

练习册系列答案
相关题目
设a>1,b>1,且a≠b,令P=lg
,Q=
,则( )
| a+b |
| 2 |
| lga+lgb |
| 2 |
| A、P<Q | B、P=Q |
| C、P>Q | D、P与Q的大小不确定 |
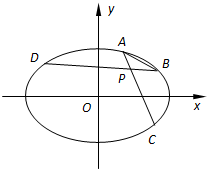 如图所示,在平面直角坐标系xOy中,设椭圆E:
如图所示,在平面直角坐标系xOy中,设椭圆E: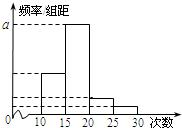 对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如图:
对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如图: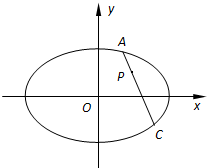 如图所示,在平面直角坐标系xOy中,过椭圆E:
如图所示,在平面直角坐标系xOy中,过椭圆E: