题目内容
已知数列{an}满足Sn+an=2n+1(n≥1,且n∈N*)
(1)求出a1,a2,a3的值;
(2)由(1)猜想出数列{an}的通项公式an,并用数学归纳法证明.
(1)求出a1,a2,a3的值;
(2)由(1)猜想出数列{an}的通项公式an,并用数学归纳法证明.
考点:数学归纳法,数列的概念及简单表示法,数列递推式
专题:综合题,点列、递归数列与数学归纳法
分析:(1)根据Sn+an=2n+1,代入即可求出a1,a2,a3.
(2)总结出规律求出an,然后利用归纳法进行证明,检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
(2)总结出规律求出an,然后利用归纳法进行证明,检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
解答:
解:(1)由a1+a1=2-+1,得a1=
,
由a1+a2+a2=2×2+1,得a2=
,
同理a3=
.
(2)猜测an=2-
(n∈N*)
证明:①由(1)当n=1时,a1=
命题成立;
②假设n=k时,ak=2-
成立,
则n=k+1时,由已知Sk+1+ak+1=Sk+2ak+1=2k+3,
把Sk=2k+1-ak及ak=2-
代入化简ak+1=2-
即n=k+1时,命题成立.
由①②得an=2-
(n∈N*).
| 3 |
| 2 |
由a1+a2+a2=2×2+1,得a2=
| 7 |
| 4 |
同理a3=
| 15 |
| 8 |
(2)猜测an=2-
| 1 |
| 2n |
证明:①由(1)当n=1时,a1=
| 3 |
| 2 |
②假设n=k时,ak=2-
| 1 |
| 2k |
则n=k+1时,由已知Sk+1+ak+1=Sk+2ak+1=2k+3,
把Sk=2k+1-ak及ak=2-
| 1 |
| 2k |
| 1 |
| 2k+1 |
即n=k+1时,命题成立.
由①②得an=2-
| 1 |
| 2n |
点评:此题主要考查归纳法的证明,归纳法一般三个步骤:(1)验证n=1成立;(2)假设n=k成立;(3)利用已知条件证明n=k+1也成立,从而求证,这是数列的通项一种常用求解的方法.

练习册系列答案
相关题目
设a>1,b>1,且a≠b,令P=lg
,Q=
,则( )
| a+b |
| 2 |
| lga+lgb |
| 2 |
| A、P<Q | B、P=Q |
| C、P>Q | D、P与Q的大小不确定 |
不等式x2-3x≤0的解集是( )
| A、{x|0<x≤3} |
| B、{x|0≤x<3} |
| C、{x|0≤x≤3} |
| D、{x|x≤0或x≥3} |
自然数列按如图规律排列,若2013在第m行第n个数,则
=( )
1
3 2
4 5 6
10 9 8 7
11 12 13 14 15
…
| n |
| m |
1
3 2
4 5 6
10 9 8 7
11 12 13 14 15
…
A、
| ||
B、
| ||
C、
| ||
D、
|
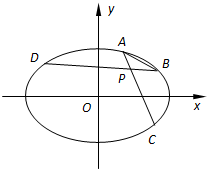 如图所示,在平面直角坐标系xOy中,设椭圆E:
如图所示,在平面直角坐标系xOy中,设椭圆E: