题目内容
已知角α的终边过点P(1,
).
(1)求sin(π-α)-sin(
+α)的值;
(2)写出满足2cosx-tanα>0的角x的集合S.
| 3 |
(1)求sin(π-α)-sin(
| π |
| 2 |
(2)写出满足2cosx-tanα>0的角x的集合S.
考点:任意角的三角函数的定义,同角三角函数基本关系的运用
专题:三角函数的求值
分析:(1)利用任意角的三角函数的定义,求出sinα,cosαd的值,化简sin(π-α)-sin(
+α),即可求解它的值;
(2)化简2cosx-tanα>0,利用余弦函数的注意直接求解角x的集合S.
| π |
| 2 |
(2)化简2cosx-tanα>0,利用余弦函数的注意直接求解角x的集合S.
解答:
解:(1)∵角α的终边过点P(1,
),可设x=1,y=
,则r=2,
∴sin α=
,cos α=
.∴sin(π-α)-sin(
+α)=sin α-cos α=
.
(2)由2cos x-tan α>0及tan α=
,得cos x>
,
由y=cos x的图象可得x的集合为:
S={x|-
+2kπ<x<
+2kπ,k∈Z}.
| 3 |
| 3 |
∴sin α=
| ||
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| ||
| 2 |
(2)由2cos x-tan α>0及tan α=
| 3 |
| ||
| 2 |
由y=cos x的图象可得x的集合为:
S={x|-
| π |
| 6 |
| π |
| 6 |
点评:本题考查任意角的三角函数的定义,诱导公式的应用,考查计算能力.

练习册系列答案
 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 某企业生产一种汽车配件,经抽样统计,该企业生产的配件尺寸的样本频率分布直方图如下.配件尺寸在[60,62)内的为一等品,尺寸在[58,60)或[62,64)内的为二等品,其余为三等品.用频率近似表示概率.
某企业生产一种汽车配件,经抽样统计,该企业生产的配件尺寸的样本频率分布直方图如下.配件尺寸在[60,62)内的为一等品,尺寸在[58,60)或[62,64)内的为二等品,其余为三等品.用频率近似表示概率.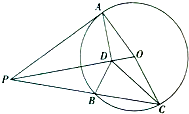 如图,AP是圆O的切线,A是切点,AD⊥OP与D点,过点P作圆O的割线与圆O相交于B,C两点
如图,AP是圆O的切线,A是切点,AD⊥OP与D点,过点P作圆O的割线与圆O相交于B,C两点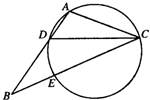 如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC
如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC 如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有
如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有