题目内容
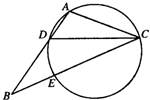 如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC
如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC(Ⅰ)求证:BE=2AD;
(Ⅱ)当AC=3,EC=6时,求AD的长.
考点:与圆有关的比例线段
专题:选作题,立体几何
分析:(Ⅰ)连接DE,证明△DBE∽△CBA,利用AB=2AC,结合角平分线性质,即可证明BE=2AD;
(Ⅱ)根据割线定理得BD•BA=BE•BC,从而可求AD的长.
(Ⅱ)根据割线定理得BD•BA=BE•BC,从而可求AD的长.
解答:
 (Ⅰ)证明:连接DE,
(Ⅰ)证明:连接DE,
∵ACED是圆内接四边形,
∴∠BDE=∠BCA,
又∠DBE=∠CBA,∴△DBE∽△CBA,即有
=
,
又∵AB=2AC,∴BE=2DE,
∵CD是∠ACB的平分线,∴AD=DE,
∴BE=2AD;…(5分)
(Ⅱ)解:由条件知AB=2AC=6,设AD=t,
则BE=2t,BC=2t+6,
根据割线定理得BD•BA=BE•BC,
即(6-t)×6=2t•(2t+6),即2t2+9t-18=0,
解得t=
或-6(舍去),则AD=
.…(10分)
 (Ⅰ)证明:连接DE,
(Ⅰ)证明:连接DE,∵ACED是圆内接四边形,
∴∠BDE=∠BCA,
又∠DBE=∠CBA,∴△DBE∽△CBA,即有
| BE |
| BA |
| DE |
| CA |
又∵AB=2AC,∴BE=2DE,
∵CD是∠ACB的平分线,∴AD=DE,
∴BE=2AD;…(5分)
(Ⅱ)解:由条件知AB=2AC=6,设AD=t,
则BE=2t,BC=2t+6,
根据割线定理得BD•BA=BE•BC,
即(6-t)×6=2t•(2t+6),即2t2+9t-18=0,
解得t=
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查三角形相似,考查角平分线性质、割线定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
已知复数z=i2,则z的虚部为( )
| A、i | B、1 | C、-1 | D、0 |