题目内容
已知直线l1：ax+3y-2=0与l2：（a-1）x+ay=0垂直，则a等于（ ）
| A、-2 | B、-1 |
| C、0或-2 | D、-2或-1 |
考点：直线的一般式方程与直线的垂直关系
专题：直线与圆
分析：利用两条直线A1x+B1y+C1=0，A2x+B2y+C2=0垂直，A1A2+B1B2=0，代入计算即可．
解答：
解：∵直线l1：ax+3y-2=0与l2：（a-1）x+ay=0垂直，
∴a（a-1）+3a=0，
即a2+2a=0，
解得a=0，或a=-2；
∴a的值是0或-2．
故选：C．
∴a（a-1）+3a=0，
即a2+2a=0，
解得a=0，或a=-2；
∴a的值是0或-2．
故选：C．
点评：本题考查了直线与直线垂直的应用问题，是基础题．
练习册系列答案
相关题目
不等式
＜0的解集为（ ）
| x2 |
| x+1 |
| A、（-1，0）∪（0，+∞） |
| B、（-∞，-1）∪（0，1） |
| C、（-1，0） |
| D、（-∞，-1） |
已知函数f(x)=2asin(2x+
)+b的定义域为[0，
]，值域为[-5，1]，则函数g（x）=abx+7在[b，a]上，（ ）
| π |
| 6 |
| π |
| 2 |
| A、有最大值2 |
| B、有最小值2 |
| C、有最大值1 |
| D、有最小值1 |
下列各式中正确的是（ ）
（1）（λ•
）•
=λ•（
）=
•（λ
）
（2）|
•
|=|
|•|
|
（3）（
•
）•
=
•（
•
）
（4）（
+
）•
=
•
+
•
．
（1）（λ•
| a |
| b |
| a |
| b |
| a |
| b |
（2）|
| a |
| b |
| a |
| b |
（3）（
| a |
| b |
| c |
| a |
| b |
| c |
（4）（
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| A、（1）（3） |
| B、（2）（4） |
| C、（1）（4） |
| D、以上都不对 |
已知A={0，1}，B={x|x⊆A}，则A与B的关系正确的是（ ）
| A、A⊆B | B、A∈B |
| C、B?A | D、B⊆A |
过点A（-2，0）的直线交圆x2+y2=1交于P、Q两点，则
•
的值为（ ）
| AP |
| AQ |
| A、3 | B、1 | C、5 | D、4 |
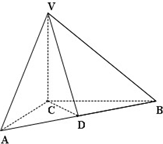如图，在三棱锥V-ABC中，VC⊥底面ABC，AC⊥BC，D为AB的中点，且AC=BC=VC=a．