题目内容
13.已知x、y∈R,且x>y>0,则( )| A. | $\frac{1}{x}-\frac{1}{y}>0$ | B. | ${(\frac{1}{2})^x}-{(\frac{1}{2})^y}<0$ | C. | log2x+log2y>0 | D. | sinx-siny>0 |
分析 根据不等式的性质判断A,根据特殊值,判断C,D,根据指数函数的性质判断B
解答 解:因为x>y>0,所以$\frac{1}{x}$<$\frac{1}{y}$,故A错误,
因为y=($\frac{1}{2}$)x为减函数,故B正确,
因为当1>x>y>0时,log2x+log2y=log2xy<0,故C错误,
因为当x=π,y=$\frac{π}{4}$时,sinx-siny<0,故D错误,
故选:B.
点评 本题考查不等式大小的比较,关键是掌握函常用函数的性质,属于基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
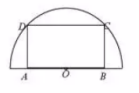 如图,在半径为40cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中A,B在直径上,点C,D在圆周上、
如图,在半径为40cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中A,B在直径上,点C,D在圆周上、