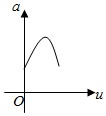题目内容
5．从单词“shadow”中任意选取4个不同的字母排成一排，则其中含有“a”的共有240种排法（用数字作答）分析 由题意知本题是一个分步计数问题，当选取4个字母时从其它5个字母中选3个，再与“a“全排列，有C53A44种结果．
解答 解：由题意知本题是一个分步计数问题，
当选取4个字母时从其它5个字母中选3个，
再与“a“全排列，C53A44=240，
即含有“a”的共有240种．
故答案为240．
点评 本题考查分步计数问题，本题解题的关键是看出要选出三个字母同所给的字母进行排列，本题是一个基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15．在三角形ABC中，$sinA=\frac{4}{5}，cosB=\frac{5}{13}$，则cosC=（ ）
| A． | $\frac{33}{65}$或$\frac{63}{65}$ | B． | $\frac{63}{65}$ | C． | $\frac{33}{65}$ | D． | 以上都不对 |
16．设f（x）=5|x|-$\frac{1}{1+{x}^{2}}$，则使得f（2x+1）＞f（x）成立的x取值范围是（ ）
| A． | （-1，-$\frac{1}{3}$） | B． | （-3，-1） | C． | （-1，+∞） | D． | （-∞，-1）∪（-$\frac{1}{3}$，+∞） |
13．已知x、y∈R，且x＞y＞0，则（ ）
| A． | $\frac{1}{x}-\frac{1}{y}＞0$ | B． | ${（\frac{1}{2}）^x}-{（\frac{1}{2}）^y}＜0$ | C． | log2x+log2y＞0 | D． | sinx-siny＞0 |
10．若a、b为实数，则“a＜1”是“$\frac{1}{a}＞1$”的（ ）条件．
| A． | 充要 | B． | 充分不必要 | ||
| C． | 必要不充分 | D． | 既不充分也不必要 |
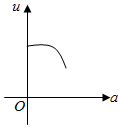
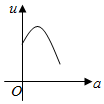
如图，有一直角墙角，两边的长度足够长，若P处有一棵树与两墙的距离分别是4m和am（0＜a＜12），不考虑树的粗细．现用16m长的篱笆，借助墙角围成一个矩形花圃ABCD．设此矩形花圃的最大面积为u，若将这棵树围在矩形花圃内，则函数u=f（a）（单位m2）的图象大致是（ ）
