题目内容
已知五条线段的长度分别为2,3,4,5,6,若从中任选三条,则能构成三角形的概率为 .
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:利用列举法就可以求出任意三条线段可以组成的组数.再根据三角形三边关系定理确定能构成三角形的组数,就可求出概率.
解答:
解:从五条线段中任选三条共有:
2,3,4;2,3,5;2,3,6;2,4,5;2,4,6;
2,5,6;3,4,5;3,4,6;3,5,6;4,5,6.
共10种情况.
根据三角形的三边关系:任意两边之和大于第三边,任意两边之差小于第三边.
其中能构成三角形的有2,3,4;2,4,5;2,5,6;3,4,5;3,4,6;3,5,6;4,5,67种情况,
故能构成三角形的概率为概率是
.
故答案为:
;
2,3,4;2,3,5;2,3,6;2,4,5;2,4,6;
2,5,6;3,4,5;3,4,6;3,5,6;4,5,6.
共10种情况.
根据三角形的三边关系:任意两边之和大于第三边,任意两边之差小于第三边.
其中能构成三角形的有2,3,4;2,4,5;2,5,6;3,4,5;3,4,6;3,5,6;4,5,67种情况,
故能构成三角形的概率为概率是
| 7 |
| 10 |
故答案为:
| 7 |
| 10 |
点评:注意分析任取三条的总情况,再分析构成三角形的情况,从而求出构成三角形的概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
执行如图所示的程序框图,输出s的值等于( )


| A、98 | B、100 |
| C、2450 | D、2550 |
如图是一个算法的程序框图,当输入的x值为5时,输出y的结果恰好是
,则①处的关系式是( )

| 1 |
| 3 |

A、y=x
| ||
| B、y=x-3 | ||
| C、y=3x | ||
| D、y=x3 |
设角α∈(0,
),角β=10°,且tanα=
,则α=( )
| π |
| 2 |
| 1+sinβ |
| cosβ |
| A、40° | B、50° |
| C、70° | D、80° |
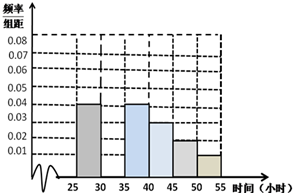 教育部,体育总局和共青团中央号召全国各级各类学校要广泛,深入地开展全国亿万大,中学生阳光体育运动,为此,某校学生会对高二年级2014年9月与10月这两个月内参加体育运动的情况进行统计,随机抽取了100名学生作为样本,得到这100名学生在该月参加体育运动总时间的小时数,根据此数据作出了如下的频数和频率的统计表和 频率分布直方图:
教育部,体育总局和共青团中央号召全国各级各类学校要广泛,深入地开展全国亿万大,中学生阳光体育运动,为此,某校学生会对高二年级2014年9月与10月这两个月内参加体育运动的情况进行统计,随机抽取了100名学生作为样本,得到这100名学生在该月参加体育运动总时间的小时数,根据此数据作出了如下的频数和频率的统计表和 频率分布直方图: