题目内容
2.已知正三棱锥P-ABC的侧棱长为2,若二面角P-AB-C的余弦值为$\frac{{\sqrt{13}}}{13}$,则三棱锥P-ABC的体积为( )| A. | $\frac{3}{4}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{{2\sqrt{6}}}{3}$ |
分析 设棱锥底面边长为a,根据二面角的大小列方程解出a,求出棱锥的高,代入棱锥的体积公式计算.
解答  解:作PO⊥底面ABC,垂足为O,则O为等边三角形△ABC的中心,
解:作PO⊥底面ABC,垂足为O,则O为等边三角形△ABC的中心,
取AB的中点D,连结PD,CD,则AB⊥PD,AB⊥CD,
∴∠PDO为二面角P-AB-C的平面角.
设棱锥的底面边长为a,则PD=$\sqrt{4-\frac{{a}^{2}}{4}}$,OD=$\frac{\sqrt{3}}{2}a×\frac{1}{3}$=$\frac{\sqrt{3}}{6}a$,
∴cos∠PDO=$\frac{OD}{PD}$=$\frac{\frac{\sqrt{3}}{6}a}{\sqrt{4-\frac{{a}^{2}}{4}}}$=$\frac{\sqrt{13}}{13}$,解得a=$\sqrt{3}$,
∴PD=$\frac{\sqrt{13}}{2}$,OD=$\frac{1}{2}$,PO=$\sqrt{P{D}^{2}-O{D}^{2}}$=$\sqrt{3}$,
∴VP-ABC=$\frac{1}{3}{S}_{△ABC}•PO$=$\frac{1}{3}×\frac{1}{2}×\sqrt{3}×\sqrt{3}×sin60°×\sqrt{3}$=$\frac{3}{4}$.
故选:A.
点评 本题考查了二面角的计算,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
17.五本不同的书在书架上排成一排,其中甲,乙两本必须连排,而丙,丁两本不能连排,则不同的排法共( )
| A. | 12种 | B. | 20种 | C. | 24种 | D. | 48种 |
14.若m是2和8的等比中项,则圆锥曲线$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{m}$=1的离心率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$或$\frac{\sqrt{21}}{3}$ | D. | $\frac{\sqrt{3}}{3}$或$\frac{\sqrt{21}}{3}$ |
12.某几何体的三视图如图所示,则该几何体的体积是( )
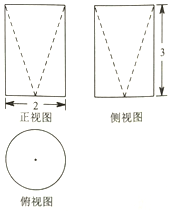

| A. | π | B. | 2π | C. | 3π | D. | 8π |