题目内容
14.若m是2和8的等比中项,则圆锥曲线$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{m}$=1的离心率是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$或$\frac{\sqrt{21}}{3}$ | D. | $\frac{\sqrt{3}}{3}$或$\frac{\sqrt{21}}{3}$ |
分析 由等比中项的概念列式求得m值,然后分m=4和m=-4求得圆锥曲线的离心率.
解答 解:∵m是2和8的等比中项,
∴m2=16,得m=±4.
若m=4,则圆锥曲线方程为$\frac{{y}^{2}}{4}+\frac{{x}^{2}}{3}=1$,表示焦点在y轴上的椭圆,
此时a=2,c=$\sqrt{{a}^{2}-{b}^{2}}=1$,椭圆离心率为e=$\frac{c}{a}=\frac{1}{2}$;
若m=-4,则圆锥曲线方程为$\frac{{x}^{2}}{3}-\frac{{y}^{2}}{4}=1$,表示焦点在x轴上的双曲线,
此时a=$\sqrt{3}$,c=$\sqrt{{a}^{2}+{b}^{2}}=\sqrt{7}$,双曲线离心率e=$\frac{\sqrt{7}}{\sqrt{3}}=\frac{\sqrt{21}}{3}$.
∴圆锥曲线$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{m}$=1的离心率是$\frac{1}{2}$或$\frac{\sqrt{21}}{3}$.
故选:C.
点评 本题考查椭圆与双曲线的标准方程,考查椭圆与双曲线的简单性质,是基础的计算题.

练习册系列答案
相关题目
5.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),x=$\sqrt{3}$y为双曲线C的一条渐近线,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | 2$\sqrt{3}$ |
2.已知正三棱锥P-ABC的侧棱长为2,若二面角P-AB-C的余弦值为$\frac{{\sqrt{13}}}{13}$,则三棱锥P-ABC的体积为( )
| A. | $\frac{3}{4}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{{2\sqrt{6}}}{3}$ |
9.已知f'(x)是奇函数f(x)的导函数,f(-1)=0,当x>0时,f′(x)<$\frac{f(x)}{x}$,则使得f(x)>0成立的x的取值范围是( )
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-1,0)∪(0,1) | D. | (-∞,-1)∪(1,+∞) |
19.某几何体的三视图如图所示,则该几何体的表面积为( )


| A. | $8+2\sqrt{5}$ | B. | $6+2\sqrt{5}$ | C. | $8+2\sqrt{3}$ | D. | $6+2\sqrt{3}$ |
4.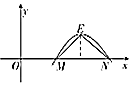 已知奇函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的导函数的部分图象如图所示,E是最高点,且△MNE是边长为1的正三角形,那么$f({\frac{1}{3}})$=( )
已知奇函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的导函数的部分图象如图所示,E是最高点,且△MNE是边长为1的正三角形,那么$f({\frac{1}{3}})$=( )
 已知奇函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的导函数的部分图象如图所示,E是最高点,且△MNE是边长为1的正三角形,那么$f({\frac{1}{3}})$=( )
已知奇函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的导函数的部分图象如图所示,E是最高点,且△MNE是边长为1的正三角形,那么$f({\frac{1}{3}})$=( )| A. | $-\frac{{\sqrt{3}}}{2π}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $-\frac{3}{4π}$ |
 如图,四棱锥P-ABCD的一个侧面PAD为等边三角形,且平面PAD⊥平面ABCD,四边形ABCD是平行四边形,AD=2,AB=4,BD=2$\sqrt{3}$
如图,四棱锥P-ABCD的一个侧面PAD为等边三角形,且平面PAD⊥平面ABCD,四边形ABCD是平行四边形,AD=2,AB=4,BD=2$\sqrt{3}$