Question

三棱锥ABCD中，BC=DC=AB=AD=

2

，BD=2，平面ABD⊥平面BCD，O为BD的中点，P、Q分别为线段AO，BC上的动点，且AP=CQ，求三棱锥PQCO体积的最大值．

Answer 1

考点：棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：如图所示，由于BC=DC=AB=AD=

2

，BD=2，平面ABD⊥平面BCD，O为BD的中点，可得AO⊥平面BCD，AO=OC=1，∠OCB=45°．设AP=x（0＜x＜1）．利用三棱锥PQCO体积V=

1

3

•OP•S△OCQ及其基本不等式的性质即可得出．

解答： 解：如图所示，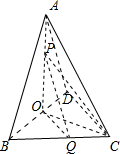
∵BC=DC=AB=AD=

2

，BD=2，平面ABD⊥平面BCD，O为BD的中点，
∴AO⊥平面BCD，
AO=OC=1，∠OCB=45°．
设AP=x（0＜x＜1）．
∴S△OCQ=

1

2

OC•CQ•sin45°=

1

2

×1•x•sin45°=

2

4

x．
∴三棱锥PQCO体积V=

1

3

•OP•S△OCQ
=

1

3

(1-x)•

2

4

x
=

2

12

x(1-x)≤

2

12

(

x+1-x

2

)2=

2

48

，当且仅当x=

1

2

时取等号．
∴三棱锥PQCO体积的最大值是

2

48

．

点评：本题考查了线面面面垂直的判定与性质定理、等腰直角三角形的性质、三棱锥的体积计算公式、基本不等式的性质，考查了推理能力与计算能力，属于中档题．