题目内容
 已知三棱柱ABC-A1B1C1,侧棱AA1垂直于底面ABC,∠BAC=90°,AB=AC=AA1=6,D为BC的中点.
已知三棱柱ABC-A1B1C1,侧棱AA1垂直于底面ABC,∠BAC=90°,AB=AC=AA1=6,D为BC的中点.(Ⅰ)若E为棱CC1的中点,求证:DE⊥A1C;
(Ⅱ)若E为棱CC1上的任意一点,求证:三棱锥A1-ADE的体积为定值,并求出此定值.γ
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的性质
专题:证明题,空间位置关系与距离
分析:(Ⅰ)连接AC1,BC1,运用线面垂直的判定和性质,即可得证;
(Ⅱ)三棱锥A1-ADE的体积即为三棱锥D-A1AE的体积.在三角形ABC中,取AC中点H,连接DH,证得DH⊥平面ACC1A1,再由棱锥的体积公式,即可得证.
(Ⅱ)三棱锥A1-ADE的体积即为三棱锥D-A1AE的体积.在三角形ABC中,取AC中点H,连接DH,证得DH⊥平面ACC1A1,再由棱锥的体积公式,即可得证.
解答:
 证明:(Ⅰ)连接AC1,BC1,
证明:(Ⅰ)连接AC1,BC1,
则由D为BC的中点,E为棱CC1的中点,则DE∥BC1,
正方形ACC1A1中,AC1⊥A1C,
侧棱AA1垂直于底面ABC,则AA1⊥AB,
又AB⊥AC,则有AB⊥平面ACC1A1,
则AB⊥A1C,即有A1C⊥平面ABC1,
则A1C⊥BC1,由于DE∥BC1,
则DE⊥A1C;
(Ⅱ)三棱锥A1-ADE的体积即为三棱锥D-A1AE的体积.
在三角形ABC中,取AC中点H,连接DH,DH∥AB,
由于AB⊥平面ACC1A1,即有DH⊥平面ACC1A1,
则三棱锥D-A1AE的体积
×DH×
AC•AA1=
×3×
×6×6=18.
则三棱锥A1-ADE的体积为定值,且为18.
 证明:(Ⅰ)连接AC1,BC1,
证明:(Ⅰ)连接AC1,BC1,则由D为BC的中点,E为棱CC1的中点,则DE∥BC1,
正方形ACC1A1中,AC1⊥A1C,
侧棱AA1垂直于底面ABC,则AA1⊥AB,
又AB⊥AC,则有AB⊥平面ACC1A1,
则AB⊥A1C,即有A1C⊥平面ABC1,
则A1C⊥BC1,由于DE∥BC1,
则DE⊥A1C;
(Ⅱ)三棱锥A1-ADE的体积即为三棱锥D-A1AE的体积.
在三角形ABC中,取AC中点H,连接DH,DH∥AB,
由于AB⊥平面ACC1A1,即有DH⊥平面ACC1A1,
则三棱锥D-A1AE的体积
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
则三棱锥A1-ADE的体积为定值,且为18.
点评:本题考查空间直线和平面垂直的性质和判定定理及运用,考查三棱锥的体积和等积法的运用,考查运算和推理能力,属于中档题.

练习册系列答案
相关题目
执行如图所示的程序框图,若输入a的值为2,则输出p的值是( )


| A、2 | ||
B、
| ||
| C、3 | ||
| D、4 |
已知c是椭圆C:
+
=1(a>b>0)的半焦距,则
的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| a |
| b+c |
A、[
| ||||
B、[
| ||||
C、(0,
| ||||
D、(
|
 如图是某粮食烘干设备的简易图,它是由两个完全一样的四棱锥P1-ABCD与P2-ABCD组成,四边形ABCD是边长为a的正方形,O1、O2分别是BC、AD的中点,P1O2⊥面ABCD,P2O1⊥面ABCD,且P1O2=P2O1=a,设备工作时,粮食从两个四棱两端的非公共部分流入烘干设备,烘干后粮食自动流到公共部分,要使这个粮食烘干设备一次烘干粮食的体积不小于45个单位体积,求a的最小值.
如图是某粮食烘干设备的简易图,它是由两个完全一样的四棱锥P1-ABCD与P2-ABCD组成,四边形ABCD是边长为a的正方形,O1、O2分别是BC、AD的中点,P1O2⊥面ABCD,P2O1⊥面ABCD,且P1O2=P2O1=a,设备工作时,粮食从两个四棱两端的非公共部分流入烘干设备,烘干后粮食自动流到公共部分,要使这个粮食烘干设备一次烘干粮食的体积不小于45个单位体积,求a的最小值.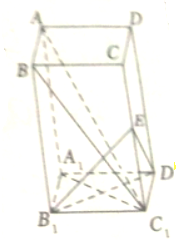 在长方体ABCD-A1B1C1D1中,E∈CC1,B1E⊥BC1,AB=CD,求证:AC1⊥面B1ED1.
在长方体ABCD-A1B1C1D1中,E∈CC1,B1E⊥BC1,AB=CD,求证:AC1⊥面B1ED1.