题目内容
设m，n是两条不同的直线，α，β是两个不同的平面，有下列四个命题：其中正确命题的序号是（ ）
①若m?β，α⊥β则m⊥α；
②若m?β，α∥β，则m∥α；
③若m⊥α，m⊥β，n⊥α，则n⊥β；
④若m∥α，m∥β，n∥α，则n∥β．
①若m?β，α⊥β则m⊥α；
②若m?β，α∥β，则m∥α；
③若m⊥α，m⊥β，n⊥α，则n⊥β；
④若m∥α，m∥β，n∥α，则n∥β．
| A、③④ | B、①② | C、②④ | D、②③ |
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：通过举反例可得①④不正确，利用两个平面平行的性质可得②正确，利用两个平面平行的判定、平行平面的性质可得③正确，从而得出结论．
解答：
解：①不对，也可能m∥α；
根据两个平面平行的性质可得②正确；
若m⊥α，m⊥β，则α∥β；再根据n⊥α，可得n⊥β，故③正确；
④不正确，由条件知，也可能n?β，
故选：D．
根据两个平面平行的性质可得②正确；
若m⊥α，m⊥β，则α∥β；再根据n⊥α，可得n⊥β，故③正确；
④不正确，由条件知，也可能n?β，
故选：D．
点评：本题主要考查空间两条直线的位置关系，直线和平面的位置关系，通过举反例，来说明某个结论不正确，是一种简单有效的方法，属于基础题．
练习册系列答案
相关题目
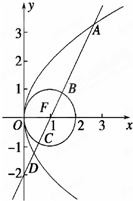已知抛物线M：y2=4x，圆F：（x-1）2+y2=1，过点F作直线l，自上而下依次与上述两曲线交于点A，B，C，D（如图所示），T（-1，0）．
某几何体三视图如图所示，其中正视图和侧视图都是等腰梯形，且上底长为2，下底长为4，腰长为