题目内容
在数列{an}中,a1=3,an+1=an+ln(1+
)(n∈N*)则an= .
| 1 |
| n |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:利用累加法和对数的运算性质可计算出结果.
解答:
解∵a1=3,an+1=an+ln(1+
)(n∈N*),
∴an+1-an=ln(1+
),
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=ln(1+
)+ln(1+
)+…+ln(1+1)+ln3,
=ln(
×
×…×2)+3
=3+lnn,
故答案为:3+lnn,
| 1 |
| n |
∴an+1-an=ln(1+
| 1 |
| n |
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=ln(1+
| 1 |
| n-1 |
| 1 |
| n-2 |
=ln(
| n |
| n-1 |
| n-1 |
| n-2 |
=3+lnn,
故答案为:3+lnn,
点评:本题主要考查数列的递推公式,明确递推公式与通项公式的异同;会根据数列的递推公式写出通项

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知c是椭圆C:
+
=1(a>b>0)的半焦距,则
的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| a |
| b+c |
A、[
| ||||
B、[
| ||||
C、(0,
| ||||
D、(
|
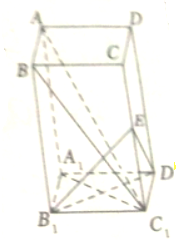 在长方体ABCD-A1B1C1D1中,E∈CC1,B1E⊥BC1,AB=CD,求证:AC1⊥面B1ED1.
在长方体ABCD-A1B1C1D1中,E∈CC1,B1E⊥BC1,AB=CD,求证:AC1⊥面B1ED1.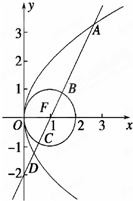 已知抛物线M:y2=4x,圆F:(x-1)2+y2=1,过点F作直线l,自上而下依次与上述两曲线交于点A,B,C,D(如图所示),T(-1,0).
已知抛物线M:y2=4x,圆F:(x-1)2+y2=1,过点F作直线l,自上而下依次与上述两曲线交于点A,B,C,D(如图所示),T(-1,0).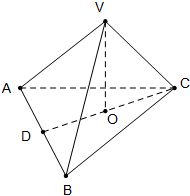 如图,棱锥V-ABC中,VO⊥平面ABC,O∈CD,VA=VB,AD=BD.求证:
如图,棱锥V-ABC中,VO⊥平面ABC,O∈CD,VA=VB,AD=BD.求证: