题目内容
设△ABC的内角A,B,C所对的边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为 ( )
| A、直角三角形 | B、锐角三角形 |
| C、钝角三角形 | D、不确定 |
考点:三角形的形状判断
专题:解三角形
分析:根据正弦定理把已知等式中的边转化为角的正弦,利用两角和公式化简求得sinA的值进而求得A,判断出三角形的形状.
解答:
解:∵bcosC+ccosB=asinA,
∴sinBcosC+sinCcosB=sin(B+C)=sinA=sin2A,
∵sinA≠0,
∴sinA=1,A=
,
故三角形为直角三角形,
故选:A.
∴sinBcosC+sinCcosB=sin(B+C)=sinA=sin2A,
∵sinA≠0,
∴sinA=1,A=
| π |
| 2 |
故三角形为直角三角形,
故选:A.
点评:本题主要考查了正弦定理的应用,解题的关键时利用正弦定理把等式中的边转化为角的正弦,属于基本知识的考查.

练习册系列答案
相关题目
具有性质:f(
)=-f(x)的函数,我们称为满足“倒负”交换的函数,则下列函数:①y=x-
;②y=x+
;③y=lnx;④y=
中所有满足“到负”交换的函数是( )
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
|
| A、①③ | B、②④ | C、①④ | D、①③④ |
把函数y=cosx的图象上的所有点的横坐标缩小到原来的一半(纵坐标不变),然后把图象向左平移
个单位,则所得图形对应的函数解析式为( )
| π |
| 8 |
A、y=cos(
| ||||
B、y=cos(2x+
| ||||
C、y=cos(
| ||||
D、y=cos(
|
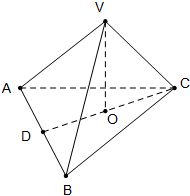 如图,棱锥V-ABC中,VO⊥平面ABC,O∈CD,VA=VB,AD=BD.求证:
如图,棱锥V-ABC中,VO⊥平面ABC,O∈CD,VA=VB,AD=BD.求证: