题目内容
1．某四棱锥的三视图如图所示，则该四棱锥的侧面积为（ ）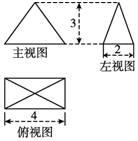
| A． | 8 | B． | 8+4$\sqrt{10}$ | C． | 2$\sqrt{10}$+$\sqrt{13}$ | D． | 4$\sqrt{10}$+2$\sqrt{13}$ |
分析 首先还原几何体为四棱锥是直观图，根据图中数据求侧面积．
解答 
解：由三视图得到几何体的直观图如图：四棱锥P-ABCD，其中OP=3，AB=CD=4，AD=BC=2，
所以PE=$\sqrt{{3}^{2}+{1}^{2}}=\sqrt{10}$，PF=$\sqrt{{2}^{2}+{3}^{2}}=\sqrt{13}$，
所以侧面积为2（S△PAB+S△PBC）=$4\sqrt{10}+2\sqrt{13}$；
故选：D．
点评 本题考查了由几何体的三视图求表面积；关键是正确还原几何体．
练习册系列答案
相关题目
11．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$夹角为$\frac{π}{3}$，|$\overrightarrow{b}$|=2，对任意x∈R，有|$\overrightarrow{b}+x\overrightarrow{a}$|≥|$\overrightarrow{a}-\overrightarrow{b}$|，则|t$\overrightarrow{b}$-$\overrightarrow{a}$|+|t$\overrightarrow{b}$-$\frac{\overrightarrow{a}}{2}$|（t∈R）的最小值是（ ）
| A． | $\frac{\sqrt{13}}{2}$ | B． | $\frac{3}{2}$ | C． | 1+$\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{7}}{2}$ |
9．已知函数f（x）=ex（2x-1）-a（x-1）有两个不同的零点，则实数a的取值范围是（ ）
| A． | （-∞，1） | B． | （0，1） | C． | （4e${\;}^{\frac{3}{2}}$，+∞） | D． | （0，1）∪（4e${\;}^{\frac{3}{2}}$，+∞） |
如图，正方体ABCD-A1B1C1D1的棱长为1，M，N分别是线段A1C1和BD上的动点，则下列判断正确的是①③④⑤（把你认为正确的序号都填上）
6．函数f（x）=lnx-4x+1的递增区间为（ ）
| A． | （0，$\frac{1}{4}$） | B． | （0，4） | C． | （-∞，$\frac{1}{4}$） | D． | （$\frac{1}{4}$，+∞） |
10．已知点M（x，y）是圆C：x2+y2-2x=0的内部任意一点，则点M满足y≥x的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{π-2}{4}$ | C． | $\frac{1}{2π}$ | D． | $\frac{π-2}{4π}$ |