题目内容
12.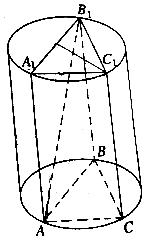 如图,圆柱有一个高6$\sqrt{2}$cm,体积为54$\sqrt{6}$cm3的内接正三棱柱ABC-A1B1C1.
如图,圆柱有一个高6$\sqrt{2}$cm,体积为54$\sqrt{6}$cm3的内接正三棱柱ABC-A1B1C1.求:(1)圆柱的体积;
(2)AC1与正三棱柱的侧面ABB1A1所成角的大小.
分析 (1)设出正三棱柱的底面边长,由体积求出底面边长,利用正弦定理求得圆柱的底面半径,则圆柱体积可求;
(2)取A1B1 中点O,连接AO,C1O,则∠AOC1为直线AC1与平面ABB1A1所成角.然后求解直角三角形得答案.
解答 解:(1)设正三棱柱ABC-A1B1C1的底面边长为a,则底面积为S=$\frac{1}{2}a×\frac{\sqrt{3}}{2}a=\frac{\sqrt{3}}{4}{a}^{2}$,
∴$V=\frac{\sqrt{3}}{4}{a}^{2}×6\sqrt{2}=54\sqrt{6}$,解得:a=6.
设圆柱的底面半径为r,则$\frac{a}{sin60°}=2r$,即$\frac{6}{\frac{\sqrt{3}}{2}}=2r$,得r=2$\sqrt{3}$.
∴圆柱的底面积为$π•(2\sqrt{3})^{2}=12π$,
则圆柱的体积为V=12$π×6\sqrt{2}=72\sqrt{2}π$;
(2)由(1)知,正三棱柱底面边长为6,侧棱长为$6\sqrt{2}$,
取A1B1 中点O,连接AO,C1O,则∠AOC1为直线AC1与平面ABB1A1所成角.
在Rt△OAC1中,AO=$\sqrt{(6\sqrt{2})^{2}+{3}^{2}}=9$,$O{C}_{1}=\sqrt{{6}^{2}-{3}^{2}}=3\sqrt{3}$,
∴tan∠OAC1=$\frac{3\sqrt{3}}{9}=\frac{\sqrt{3}}{3}$.
∴AC1与正三棱柱的侧面ABB1A1所成角的大小为30°.
点评 本题考查线面角及多面体体积的求法,考查空间想象能力和思维能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知i为虚数单位,复数z满足z(1-i)=1+i,则z2017=( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
7.已知复数z满足$\frac{1-i}{\overline{z}}$=i(其中i为虚数单位),则z2=( )
| A. | 2i | B. | -2i | C. | 2+2i | D. | 2-2i |
1.($\sqrt{x}$-$\frac{2}{x}$)8的展开式中,x的系数为( )
| A. | -112 | B. | 112 | C. | 56 | D. | -56 |