题目内容
5.已知函数f(x)=$\left\{\begin{array}{l}{\frac{{2}^{x}+2}{2},x≤1}\\{|lo{g}_{2}(x-1)|,x>1}\end{array}\right.$,则函数F(x)=f[f(x)]-2f(x)-$\frac{3}{2}$的零点个数是3.分析 令f(x)=t,函数F(x)=f[f(x)]-2f(x)-$\frac{3}{2}$的零点个数问题?f(t)-2t-$\frac{3}{2}$=0的根的个数问题.结合图象可得f(t)-2t-$\frac{3}{2}$=0的根t1<0,t2∈(1,2).f(x)=t1无解,f(x)=t2有3解,解得得到函数F(x)=f[f(x)]-2f(x)-$\frac{3}{2}$的零点个数
解答  解:令f(x)=t,函数F(x)=f[f(x)]-2f(x)-$\frac{3}{2}$的零点个数问题?f(t)-2t-$\frac{3}{2}$=0的根的个数问题.
解:令f(x)=t,函数F(x)=f[f(x)]-2f(x)-$\frac{3}{2}$的零点个数问题?f(t)-2t-$\frac{3}{2}$=0的根的个数问题.
即y=f(t),y=2t+$\frac{3}{2}$的图象如图(1),结合图象可得f(t)-2t-$\frac{3}{2}$=0的根t1<0,t2∈(1,2).
f(x)=t1无解,f(x)=t2有3解,
综上,函数F(x)=f[f(x)]-2f(x)-$\frac{3}{2}$的零点个数是3.
故答案为:3
点评 本题考查了复合函数零点问题,解题的关键是合理利用换元思想求解,属于中档题.

练习册系列答案
相关题目
10.已知i为虚数单位,复数z满足z(1-i)=1+i,则z2017=( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
14.已知集合M={x|-1≤x≤2},N={x|1-3a<x≤2a},若M∩N=M,则实数a的取值范围是( )
| A. | ($\frac{2}{3}$,1) | B. | (1,+∞) | C. | ($\frac{2}{3}$,+∞) | D. | [1,+∞) |
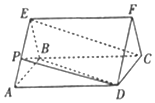 如图,三棱柱ABE-DCF中,△EAB是正三角形,四边形ABCD是矩形,且EA=2,BC=2$\sqrt{3}$,EC=4.
如图,三棱柱ABE-DCF中,△EAB是正三角形,四边形ABCD是矩形,且EA=2,BC=2$\sqrt{3}$,EC=4.