题目内容
20.已知α、β是两个平面,m、n是两条直线,则下列命题不正确的是( )| A. | 若m∥n,m⊥α,则n⊥α | B. | 若m⊥α,m⊥β,则α∥β | ||
| C. | 若m⊥α,m?β,则α⊥β | D. | 若m⊥α,α∩β=n,则m∥n |
分析 在A中,由直线与平面垂直的判定定理得n⊥α;在B中,由面面平行的判定定理得α∥β;在C中,由面面垂直的判定定理得α⊥β;在D中,m与n相交、平行或异面.
解答 解:由α、β是两个平面,m、n是两条直线,知:
在A中:若m∥n,m⊥α,则由直线与平面垂直的判定定理得n⊥α,故A正确;
在B中:若m⊥α,m⊥β,则由面面平行的判定定理得α∥β,故B正确;
在C中:若m⊥α,m?β,则由面面垂直的判定定理得α⊥β,故C正确;
在D中:若m⊥α,α∩β=n,则m与n相交、平行或异面,故D错误.
故选:D.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
相关题目
10.对任意x∈[-1,1],不等式-4≤x3+3|x-a|≤4恒成立,则实数a的取值范围为( )
| A. | [-$\frac{2}{3}$,$\frac{2}{3}$] | B. | [-$\frac{1}{3}$,$\frac{1}{3}$] | C. | [0,$\frac{2}{3}$] | D. | [0,1] |
11.已知复数z满足(2z+1)i=2,则z=( )
| A. | -1-2i | B. | -$\frac{1}{2}$+i | C. | -$\frac{1}{2}$-i | D. | $\frac{1}{2}$-i |
8.已知f(x)=$\left\{\begin{array}{l}{sinπx,x≤0}\\{2f(x-1),x>0}\end{array}\right.$,则f($\frac{4}{3}$)等于( )
| A. | 2 | B. | -2 | C. | 2$\sqrt{3}$ | D. | -2$\sqrt{3}$ |
15.设{an}是公差为正数的等差数列,若a1+a3=10,a1a3=16,则a12等于( )
| A. | 25 | B. | 30 | C. | 35 | D. | 40 |
10.二项式(2$\root{3}{x}$-$\frac{1}{\sqrt{x}}$)7的展开式中x-1项的系数是( )
| A. | 280 | B. | 35 | C. | -35 | D. | -280 |
 在正方体ABCD-A1B1C1D1中,E、F分别是AB、B1C1的中点.
在正方体ABCD-A1B1C1D1中,E、F分别是AB、B1C1的中点.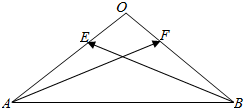 等腰△OAB中,∠A=∠B=30°,E、F分别是直线OA、OB上的动点,$\overrightarrow{OA}$、$\overrightarrow{OB}$上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AE}$•$\overrightarrow{AB}$=9,则λ=-$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.
等腰△OAB中,∠A=∠B=30°,E、F分别是直线OA、OB上的动点,$\overrightarrow{OA}$、$\overrightarrow{OB}$上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AE}$•$\overrightarrow{AB}$=9,则λ=-$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.