题目内容
12.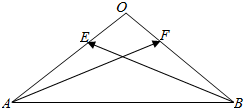 等腰△OAB中,∠A=∠B=30°,E、F分别是直线OA、OB上的动点,$\overrightarrow{OA}$、$\overrightarrow{OB}$上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AE}$•$\overrightarrow{AB}$=9,则λ=-$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.
等腰△OAB中,∠A=∠B=30°,E、F分别是直线OA、OB上的动点,$\overrightarrow{OA}$、$\overrightarrow{OB}$上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AE}$•$\overrightarrow{AB}$=9,则λ=-$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.
分析 (1)根据等腰三角形的性质解出AB,代入数量积公式求出AE,从而得出λ的值.
(2)用$\overrightarrow{OA},\overrightarrow{OB}$表示出$\overrightarrow{AF},\overrightarrow{BE}$,用μ表示出λ,计算出数量积得到关于μ得函数,求出此函数的最小值即可.
解答 解:(1)过O作OC⊥AB,则C是AB的中点,∵OA=2,∠OAB=30°,∴AC=$\sqrt{3}$,AB=2AC=2$\sqrt{3}$.
∵$\overrightarrow{AE}$•$\overrightarrow{AB}$=AE•AB•cos30°=9,∴AE=3,∴$\overrightarrow{OE}$=-$\frac{1}{2}$$\overrightarrow{OA}$,∴λ=-$\frac{1}{2}$.
(2)∵λ+2μ=2,∴λ=2-2μ.$\overrightarrow{OA}•\overrightarrow{OB}$=OA×OA×cos120°=-2.
∵$\overrightarrow{AF}$=$\overrightarrow{AO}+\overrightarrow{OF}$=-$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,$\overrightarrow{BE}$=$\overrightarrow{BO}+\overrightarrow{OE}$=-$\overrightarrow{OB}$+(2-2μ)$\overrightarrow{OA}$.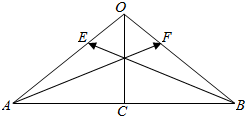
∴$\overrightarrow{AF}$•$\overrightarrow{BE}$=(-$\overrightarrow{OA}$+μ$\overrightarrow{OB}$)•(-$\overrightarrow{OB}$+(2-2μ)$\overrightarrow{OA}$)=(2μ-2)${\overrightarrow{OA}}^{2}$-μ${\overrightarrow{OB}}^{2}$+$\overrightarrow{OA}•\overrightarrow{OB}$+μ(2-2μ)$\overrightarrow{OA}•\overrightarrow{OB}$
=4(2μ-2)-4μ-2-2μ(2-2μ)=4μ2-10.
∴当μ=0时,$\overrightarrow{AF}$•$\overrightarrow{BE}$取得最小值-10.
故答案为-$\frac{1}{2}$,-10.
点评 本题考查了平面向量的数量积运算,平面向量的线性运算,函数的最值,属于中档题.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案| A. | sin11°>sin168° | B. | sin194°<cos160° | ||
| C. | cos(-$\frac{15π}{8}$)>cos$\frac{14π}{9}$ | D. | tan(-$\frac{π}{5}$)<tan(-$\frac{3π}{7}$) |
| A. | 若m∥n,m⊥α,则n⊥α | B. | 若m⊥α,m⊥β,则α∥β | ||
| C. | 若m⊥α,m?β,则α⊥β | D. | 若m⊥α,α∩β=n,则m∥n |
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |