题目内容
已知向量
=(
,1),
=(0,-1),
=(t,
),若
-2
与
共线,则t= .
| m |
| 3 |
| n |
| k |
| 3 |
| m |
| n |
| k |
考点:平面向量共线(平行)的坐标表示
专题:平面向量及应用
分析:由向量减法的坐标运算及数乘运算求得若
-2
的坐标,再由向量共线的坐标表示列式求得t的值.
| m |
| n |
解答:
解:∵
=(
,1),
=(0,-1),
∴
-2
=(
,1)-2(0,-1)=(
,3),
又
=(t,
),且
-2
与
共线,
则
×
-3t=0,解得:t=1.
故答案为:1.
| m |
| 3 |
| n |
∴
| m |
| n |
| 3 |
| 3 |
又
| k |
| 3 |
| m |
| n |
| k |
则
| 3 |
| 3 |
故答案为:1.
点评:平行问题是一个重要的知识点,在高考题中常常出现,常与向量的模、向量的坐标表示等联系在一起,要特别注意垂直与平行的区别.若
=(a1,a2),
=(b1,b2),则
⊥
?a1a2+b1b2=0,
∥
?a1b2-a2b1=0,是基础题.
| a |
| b |
| a |
| b |
| a |
| b |

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
已知函数若x,y满足约束条件
,目标函数z=ax+2y仅在点(1,0)处取得最小值,则实数a的取值范围是( )
|
| A、(-4,2) |
| B、(-4,1) |
| C、(-∞,-4)∪(2,+∞) |
| D、(-∞,-4)∪(1,+∞) |
设数列
,
,2
,
,…,则2
是这个数列的( )
| 2 |
| 5 |
| 2 |
| 11 |
| 5 |
| A、第6项 | B、第7项 |
| C、第8项 | D、第9项 |
如图是某样本数据的茎叶图,则该样本数据的众数为( )
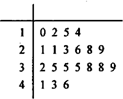

| A、10 | B、21 | C、35 | D、46 |
经过点(2,1),且倾斜角为135°的直线方程为( )
| A、x+y-3=0 |
| B、x-y-1=0 |
| C、2x-y-3=0 |
| D、x-2y=0 |
复数z=
,则z的共轭复数
在复平面内对应的点( )
| i2+i3+i4 |
| 1-i |
. |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |