题目内容
已知函数f(x)+1=
,当x∈[0,1]时,f(x)=x.若在区间x∈(-1,1]内,g(x)=f(x)-mx-m有两个零点,则实数m的取值范围是( )
| 1 |
| f(x+1) |
A、(0,
| ||
B、[
| ||
C、[0,
| ||
D、[0,
|
考点:函数零点的判定定理
专题:综合题,函数的性质及应用
分析:求出f(x)的解析式,把在区间x∈(-1,1]内,g(x)=f(x)-mx-m有两个零点,
转化为m=
有2个解,令k(x)=
,作出图象,运用图象的交点判断零点个数,
得出参变量m的取值范围.
转化为m=
| f(x) |
| x+1 |
| f(x) |
| x+1 |
得出参变量m的取值范围.
解答:
解:∵f(x)+1=
,
∴数f(x)=
-1,
∵当x∈[0,1]时,f(x)=x.
∴当x∈[-1,0]时,f(x)=
-1=
-1,
∵∴f(x)=m(x+1)有2个解
即m=
有2个解
令k(x)=
,
则k(x)=
k(x)图象如下:
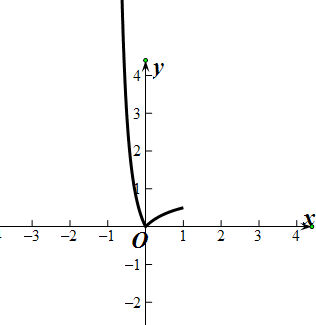
k(1)=
,
∴k(x)=
,与y=m有2个交点时,0<m≤
∴g(x)=f(x)-mx-m有两个零点,则实数m的取值范围为:(0,
],
故选:A
| 1 |
| f(x+1) |
∴数f(x)=
| 1 |
| f(x+1) |
∵当x∈[0,1]时,f(x)=x.
∴当x∈[-1,0]时,f(x)=
| 1 |
| f(x+1) |
| 1 |
| x+1 |
∵∴f(x)=m(x+1)有2个解
即m=
| f(x) |
| x+1 |
令k(x)=
| f(x) |
| x+1 |
则k(x)=
|
k(x)图象如下:
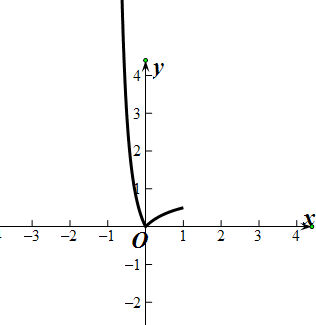
k(1)=
| 1 |
| 2 |
∴k(x)=
| f(x) |
| x+1 |
| 1 |
| 2 |
∴g(x)=f(x)-mx-m有两个零点,则实数m的取值范围为:(0,
| 1 |
| 2 |
故选:A
点评:本题综合考察了函数的图象的交点,函数的零点,方程的根的关系,考察了数形结合的思想.

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
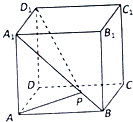 如图所示,在棱长为l的正方体ABCD-ABCD的面对角线AB上存在一点P使得AP+DP取得最小值,则此最小值为( )
如图所示,在棱长为l的正方体ABCD-ABCD的面对角线AB上存在一点P使得AP+DP取得最小值,则此最小值为( )| A、2 | ||||||
B、
| ||||||
C、2+
| ||||||
D、
|
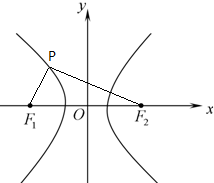 如图,若F1,F2是双曲线
如图,若F1,F2是双曲线