题目内容
11.若点P为△ABC某两边的垂直平分线的交点,且$\overrightarrow{PA}+\overrightarrow{PB}-\overrightarrow{PC}=\overrightarrow 0$,则∠ACB=( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
分析 由题意可得P为三角形ABC的外心,且$\overrightarrow{PA}$+$\overrightarrow{PB}$=$\overrightarrow{PC}$,即有四边形PBCA为菱形,且△PAC和△PBC为等边三角形,即可得到所求角.
解答 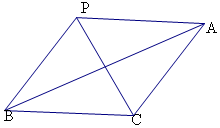 解:点P为△ABC某两边的垂直平分线的交点,
解:点P为△ABC某两边的垂直平分线的交点,
且$\overrightarrow{PA}+\overrightarrow{PB}-\overrightarrow{PC}=\overrightarrow 0$,
可得P为三角形ABC的外心,且$\overrightarrow{PA}$+$\overrightarrow{PB}$=$\overrightarrow{PC}$,
即有四边形PBCA为菱形,
且△PAC和△PBC为等边三角形,
即有∠ACB=$\frac{2π}{3}$.
故选:C.
点评 本题考查向量的平行四边形法则和三角形的外心的性质,考查数形结合思想,属于基础题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
16. 如图,阴影部分的面积为( )
如图,阴影部分的面积为( )
 如图,阴影部分的面积为( )
如图,阴影部分的面积为( )| A. | 9 | B. | $\frac{9}{2}$ | C. | $\frac{13}{6}$ | D. | $\frac{7}{3}$ |
3.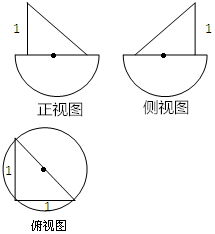 已知某几何体的三视图如图所示,其中正视图、侧视图均由直角三角形中与半圆构成,俯视图由圆和内接三角形构成,根据图中的数据可得几何体的表面积为( )
已知某几何体的三视图如图所示,其中正视图、侧视图均由直角三角形中与半圆构成,俯视图由圆和内接三角形构成,根据图中的数据可得几何体的表面积为( )
 已知某几何体的三视图如图所示,其中正视图、侧视图均由直角三角形中与半圆构成,俯视图由圆和内接三角形构成,根据图中的数据可得几何体的表面积为( )
已知某几何体的三视图如图所示,其中正视图、侧视图均由直角三角形中与半圆构成,俯视图由圆和内接三角形构成,根据图中的数据可得几何体的表面积为( )| A. | 1+$\frac{\sqrt{3}+3π}{2}$ | B. | $\frac{1+\sqrt{3}+π}{2}$ | C. | $\frac{1+\sqrt{3}+3π}{2}$ | D. | $\frac{3+\sqrt{3}+3π}{2}$ |
1.f(x)为奇函数,当x>0时,f(x)=π-arccos(sinx)则x<0时,f(x)=( )
| A. | arccos(sinx) | B. | π+arccos(sinx) | C. | -arccos(sinx) | D. | -π-arccos(sinx) |
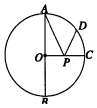 如图所示,AB为⊙O的直径,AB=2,OC是⊙O的半径,OC⊥AB,点D在$\widehat{AC}$上,$\widehat{AD}$=2$\widehat{CD}$,点P是OC上一动点,则PA+PD的最小值为$\sqrt{3}$.
如图所示,AB为⊙O的直径,AB=2,OC是⊙O的半径,OC⊥AB,点D在$\widehat{AC}$上,$\widehat{AD}$=2$\widehat{CD}$,点P是OC上一动点,则PA+PD的最小值为$\sqrt{3}$.