题目内容
设Sn为数列{an}的前n项和,Sn=kn2+n,n∈N*,其中k是常数.若对于任意的m∈N*,am,a2m,a4m成等比数列,则k的值为 .
考点:等比数列的性质
专题:等差数列与等比数列
分析:先通过求a1=S1求得a1,进而根据当n≥2时an=Sn-Sn-1求出an,验证可得an,(2)根据am,a2m,a4m成等比数列,可知a2m2=ama4m,根据数列{an}的通项公式,代入化简即可.
解答:
解:(1)由题意当n=1,a1=S1=k+1,
当n≥2,an=Sn-Sn-1=kn2+n-[k(n-1)2+(n-1)]=2kn-k+1(*).
经检验,n=1时(*)式成立,
∴an=2kn-k+1.
(2)∵am,a2m,a4m成等比数列,
∴a2m2=ama4m,
即(4km-k+1)2=(2km-k+1)(8km-k+1),
整理得:mk(k-1)=0,对任意的m∈N*成立,
∴k=0或k=1.
故答案为:k=0或k=1.
当n≥2,an=Sn-Sn-1=kn2+n-[k(n-1)2+(n-1)]=2kn-k+1(*).
经检验,n=1时(*)式成立,
∴an=2kn-k+1.
(2)∵am,a2m,a4m成等比数列,
∴a2m2=ama4m,
即(4km-k+1)2=(2km-k+1)(8km-k+1),
整理得:mk(k-1)=0,对任意的m∈N*成立,
∴k=0或k=1.
故答案为:k=0或k=1.
点评:本题考查数列等比关系的确定和求数列通项公式,属中档题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
某工厂甲、乙、丙三个车间生产同一产品,数量分别为120件,90件,60件.为了解它们的产品质量是否有显著差异,用分层抽样方法抽取了一个容量为n的样本进行调查,其中从丙车间的产品中抽取了4件,则n= .
已知直线l1:x+ky-2k=0与l2:kx-(k-2)y+1=0垂直,则k的值是( )
| A、1 | B、3 | C、1或-2 | D、0或3 |
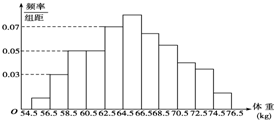 为了解某地区高三学生的身体发育情况,抽查了该地区100名高三男生的体重.根据抽样测量后的男生体重(单位:kg)数据绘制的频率分布直方图如图所示,则这100名学生中体重值在区间[56.5,64.5)的人数是
为了解某地区高三学生的身体发育情况,抽查了该地区100名高三男生的体重.根据抽样测量后的男生体重(单位:kg)数据绘制的频率分布直方图如图所示,则这100名学生中体重值在区间[56.5,64.5)的人数是