题目内容
已知函数f(x)=ax2+bx(a,b∈R),函数g(x)=lnx.
(1)当a=0时,函数f(x)的图象与函数g(x)的图象有公共点,求实数b的最大值;
(2)当b=0时,试判断函数f(x)的图象与函数g(x)的图象的公共点的个数;
(3)函数f(x)的图象能否恒在函数y=bg(x)的上方?若能,求出a,b的取值范围;若不能,请说明理由.
(1)当a=0时,函数f(x)的图象与函数g(x)的图象有公共点,求实数b的最大值;
(2)当b=0时,试判断函数f(x)的图象与函数g(x)的图象的公共点的个数;
(3)函数f(x)的图象能否恒在函数y=bg(x)的上方?若能,求出a,b的取值范围;若不能,请说明理由.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)由a=0,可得f(x)=bx,由一次函数与对数函数图象可知两图象相切时b取最大值,利用导数的几何意义即可得出;
(2)由于b=0,x>0,可得f(x)=g(x)?a=
,即原题等价于直线y=a与函数r(x)=
的图象的公共点的个数,利用导数研究函数r(x)的单调性即可得出;
(3)函数f(x)的图象恒在函数y=bg(x)的上方,即f(x)>bg(x)在x>0时恒成立.对a,b分类讨论,再利用(1)(2)的结论即可得出.
(2)由于b=0,x>0,可得f(x)=g(x)?a=
| lnx |
| x2 |
| lnx |
| x2 |
(3)函数f(x)的图象恒在函数y=bg(x)的上方,即f(x)>bg(x)在x>0时恒成立.对a,b分类讨论,再利用(1)(2)的结论即可得出.
解答:
解:(1)∵a=0,∴f(x)=bx,
由一次函数与对数函数图象可知两图象相切时b取最大值,
设切点横坐标为x0,∵f′(x)=b, g′(x)=
,
∴
, ∴x0=e,
∴b=
,即实数b的最大值为b=
;
(2)∵b=0,x>0,
∴f(x)=g(x)?a=
,
即原题等价于直线y=a与函数r(x)=
的图象的公共点的个数,
∵r′(x)=
=
,
由r′(x)>0,解得0<x<
,∴r(x)在(0,
)单调递增,且r(x)∈(-∞,
);
由r′(x)<0,解得x>
,∴r(x)在(
,+∞)单调递减,且r(x)∈(0,
).
∴a∈(
,+∞)时,无公共点;a∈(-∞,0]∪{
}时,有一个公共点;a∈(0,
)时,有两个公共点.
(3)函数f(x)的图象恒在函数y=bg(x)的上方,
即f(x)>bg(x)在x>0时恒成立,
①当a<0时,f(x)图象开口向下,即f(x)>bg(x)在x>0时不可能恒成立,
②a=0时,bx>blnx,由(1)可得x>lnx,
∴b>0时,f(x)>bg(x)恒成立,b≤0时,f(x)>bg(x)不成立,
③a>0时,
若b<0,则
<
,由(2)可得
无最小值,故f(x)>bg(x)不可能恒成立,
若b=0,则ax2>0,故f(x)>bg(x)恒成立,
若b>0,则ax2+b(x-lnx)>0,故f(x)>bg(x)恒成立,
综上,a=0,b>0或a>0,b≥0时
函数f(x)的图象恒在函数y=bg(x)的图象的上方.
由一次函数与对数函数图象可知两图象相切时b取最大值,
设切点横坐标为x0,∵f′(x)=b, g′(x)=
| 1 |
| x |
∴
|
∴b=
| 1 |
| e |
| 1 |
| e |
(2)∵b=0,x>0,
∴f(x)=g(x)?a=
| lnx |
| x2 |
即原题等价于直线y=a与函数r(x)=
| lnx |
| x2 |
∵r′(x)=
| x-2xlnx |
| x4 |
| 1-2lnx |
| x3 |
由r′(x)>0,解得0<x<
| e |
| e |
| 1 |
| 2e |
由r′(x)<0,解得x>
| e |
| e |
| 1 |
| 2e |
∴a∈(
| 1 |
| 2e |
| 1 |
| 2e |
| 1 |
| 2e |
(3)函数f(x)的图象恒在函数y=bg(x)的上方,
即f(x)>bg(x)在x>0时恒成立,
①当a<0时,f(x)图象开口向下,即f(x)>bg(x)在x>0时不可能恒成立,
②a=0时,bx>blnx,由(1)可得x>lnx,
∴b>0时,f(x)>bg(x)恒成立,b≤0时,f(x)>bg(x)不成立,
③a>0时,
若b<0,则
| a |
| b |
| lnx-x |
| x2 |
| lnx-x |
| x2 |
若b=0,则ax2>0,故f(x)>bg(x)恒成立,
若b>0,则ax2+b(x-lnx)>0,故f(x)>bg(x)恒成立,
综上,a=0,b>0或a>0,b≥0时
函数f(x)的图象恒在函数y=bg(x)的图象的上方.
点评:本题考查了利用导数研究函数的单调性极值与最值、导数的几何意义,考查了分类讨论的思想方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
△ABC中,若sin2A+sin2B>sin2C,则△ABC是( )
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不确定 |
已知正项数列{an}中,a1=1,a2=2,2an2=an+12+an-12(n≥2),则a22等于( )
| A、16 | ||
| B、8 | ||
C、2
| ||
| D、4 |
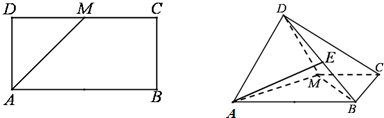 如图,已知矩形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
如图,已知矩形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.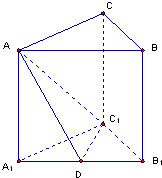 如图,直三棱柱ABC-A1B1C1底面是等腰三角形(侧棱垂直于底面的棱柱叫直棱柱),A1C1=C1B1,D是线段A1B1的中点.
如图,直三棱柱ABC-A1B1C1底面是等腰三角形(侧棱垂直于底面的棱柱叫直棱柱),A1C1=C1B1,D是线段A1B1的中点.