题目内容
2.若向量$\overrightarrow a$与$\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=2,($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{a}$则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值为$\frac{\sqrt{2}}{2}$.分析 利用向量的垂直关系求解即可.
解答 解:向量$\overrightarrow a$与$\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=2,($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{a}$,
可得:($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=0,
即:${\overrightarrow{a}}^{2}$$-\left|\overrightarrow{a}\right|\left|\overrightarrow{b}\right|cos<\overrightarrow{a},\overrightarrow{b}>$=0,
2-$\sqrt{2}×2$$cos<\overrightarrow{a},\overrightarrow{b}>$=0,
解得$cos<\overrightarrow{a},\overrightarrow{b}>$=$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查斜率的数量积的应用,基本知识的考查.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
7.设复数z满足(1+2i)z=5i,则复数z为( )
| A. | 2+i | B. | -2+i | C. | 2-i | D. | -2-i |
12.设p:“$\frac{a-1}{a-2}$≥0”,q:“圆x2+y2=a2(a>0)与直线3x+4y-5=0相交且与圆(x+3)2+(y+4)2=9外离”,则¬p是q的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
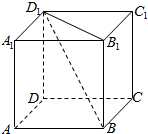 已知正方体ABCD-A1B1C1D1的棱长为a,
已知正方体ABCD-A1B1C1D1的棱长为a,