题目内容
13.函数f(x)的定义域为R,并满足以下条件:①对任意x∈R,有f(x)>0; ②对任意x、y∈R,有f(xy)=[f(x)]y; ③f($\frac{1}{3}$)>1
(1)求f(0)的值;
(2)判断f(x)的在R上单调性并说明理由;
(3)若f(2)=2,且x满足f($\frac{1}{2}$)≤f(x)≤f(2),求函数y=2f(2log2x)+$\frac{1}{{f(2{{log}_2}x)}}$的最大值和最小值.
分析 (1)根据条件f(xy)=[f(x)]y;令x=$\frac{1}{3}$,y=0,可得f(0),
(2)利用赋值法求f(1),然后根据指数函数的性质确定函数的单调性.
(3)利用换元法和导数法,判断函数的最值进行求解即可.
解答 解:(1)因为f(x)>0,任意的x,y∈R,f(xy)=[f(x)]y,所以令x=$\frac{1}{3}$,y=0,
则f(0)=[f($\frac{1}{3}$)]0=1,即f(0)=1.
(2)令$x=\frac{1}{3},y=3$得$f(1)=f(\frac{1}{3}×3)={[f(\frac{1}{3})]}^{3}$,因为f($\frac{1}{3}$)>1,所以$f(1)=f(\frac{1}{3}×3)={[f(\frac{1}{3})]}^{3}>1$.
令x=1,则f(xy)=f(y)=[f(1)]y,
即f(x)=[f(1)]x,为底数大于1的指数函数,所以函数f(x)在R上单调递增.
(3)∵函数f(x)在R上单调递增,
∴由f($\frac{1}{2}$)≤f(x)≤f(2),得$\frac{1}{2}$≤x≤2,
由$\frac{1}{2}$≤2log2x≤2,得$\frac{1}{4}$≤log2x≤1,
令t=log2x,则$\frac{1}{4}$≤t≤1,
若f(2)=2,则f(2)=[f(1)]2=2,即f(1)=$\sqrt{2}$,
则f(x)=($\sqrt{2}$)x,
则函数等价为y=2f(2t)+$\frac{1}{f(2t)}$=2•($\sqrt{2}$)2t+$\frac{1}{(\sqrt{2})^{2t}}$=2•2t+$\frac{1}{{2}^{t}}$,
再设m=2t,则${2}^{\frac{1}{4}}$≤m≤2,
则函数等价为y=2m+$\frac{1}{m}$,则y′=2-$\frac{1}{{m}^{2}}$=$\frac{2{m}^{2}-1}{{m}^{2}}$,
由y′=0得2m2-1=0得m=$\frac{\sqrt{2}}{2}$,
则当m=$\frac{\sqrt{2}}{2}$时,函数y=2m+$\frac{1}{m}$取得极小值同时也是最小值为y=$2×\frac{\sqrt{2}}{2}+\frac{1}{\frac{\sqrt{2}}{2}}$=$\sqrt{2}+\sqrt{2}=2\sqrt{2}$,
当m=2时,y=4+$\frac{1}{2}$=$\frac{9}{2}$,
当m=${2}^{\frac{1}{4}}$时,y=2•${2}^{\frac{1}{4}}$+$\frac{1}{{2}^{\frac{1}{4}}}$=${2}^{\frac{5}{4}}$+${2}^{-\frac{1}{4}}$<$\frac{9}{2}$,
故函数的最大值为$\frac{9}{2}$,最小值为2$\sqrt{2}$.
点评 本题主要考查抽象函数的应用和性质,利用赋值法是解决抽象函数的基本方法,综合性较强,运算量较大.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{6}{125}$ | a | b | $\frac{24}{125}$ |
(2)求ξ的数学期望E(ξ).
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{7}$ | D. | $\frac{2\sqrt{3}}{3}$ |
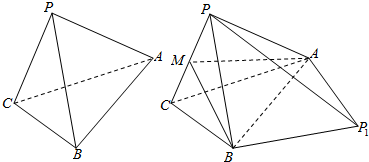 如图1,四面体PABC中,BC=BP=1,AC=AP=$\sqrt{3}$,AB=2,将△PAB沿直线AB翻折至△P1AB,使点A,P1,B,C在同一平面内(如图2),点M为PC中点.
如图1,四面体PABC中,BC=BP=1,AC=AP=$\sqrt{3}$,AB=2,将△PAB沿直线AB翻折至△P1AB,使点A,P1,B,C在同一平面内(如图2),点M为PC中点.