题目内容
已知f（x）=-lnx，g（x）=
-1（x＞0）
（Ⅰ）求F（x）=f（x）-g（x）的极值，并证明：若x1，x2∈（0，+∞）有f（x2）-f（x1）≥f′（x1）（x2-x1）
（Ⅱ）设λ1，λ2＞0，且λ1+λ2=1，x1＞0，x2＞0，证明：λ1f（x1）+λ2f（x2）≥f（λ1x1+λ2x2）．若λi＞0，xi＞0，（i=1，2，…n），由上述结论猜想一个一般性结论（不需证明）．
（Ⅲ）证明：若ai＞0（i=1，2，…n），则a1 a1a2 a2…an an≥(
)a1+a2+…+an．
| 1 |
| x |
（Ⅰ）求F（x）=f（x）-g（x）的极值，并证明：若x1，x2∈（0，+∞）有f（x2）-f（x1）≥f′（x1）（x2-x1）
（Ⅱ）设λ1，λ2＞0，且λ1+λ2=1，x1＞0，x2＞0，证明：λ1f（x1）+λ2f（x2）≥f（λ1x1+λ2x2）．若λi＞0，xi＞0，（i=1，2，…n），由上述结论猜想一个一般性结论（不需证明）．
（Ⅲ）证明：若ai＞0（i=1，2，…n），则a1 a1a2 a2…an an≥(
| a1+a2+…+an |
| n |
考点：利用导数求闭区间上函数的最值,利用导数研究函数的极值
专题：导数的综合应用
分析：（Ⅰ）利用导数求函数的极值即可，F（x）max=F（0）=0；∴当x＞0时，f （x）≤g（x） 恒成立，即 x＞0时 lnx≥1-
恒成立，利用该结论即可证得原命题成立；
（Ⅱ）利用（Ⅰ）的结论证明即可得出结论成立；
（Ⅲ）利用（Ⅱ）的结论结合对数的运算性质即可得出结论．
| 1 |
| x |
（Ⅱ）利用（Ⅰ）的结论证明即可得出结论成立；
（Ⅲ）利用（Ⅱ）的结论结合对数的运算性质即可得出结论．
解答：
解：（1）F（x）=-lnx-
+1，则F′（x）=
当x∈（0，1）时F′（x）＞0，x∈（1，+∞）时F′（x）＜0
∴F（x）在（0，1）递增，在（1，+∞）递减，
∴当x=1时，函数有极大值为F（1）=0，
∴F（x）max=F（0）=0；∴当x＞0时，f （x）≤g（x） 恒成立，即 x＞0时 lnx≥1-
恒成立．
∴f （x2）-f （x1）=ln
≥1-
=-
（x2-x1）=f′（x1）（x2-x1）
（2）证明：设λ1＞0，λ2＞0且λ1+λ2=1
令x3=λ1 x1+λ2 x2，则x3＞0且x1-x3=λ2（x1-x2） x2-x3=λ1（x2-x1）
由（1）知f （x1）-f （x3）≥f′（x3）（ x1-x3）=λ2 f′（x3）（ x1-x2） …①
f （x2）-f （x3）≥f′（x3）（ x2-x3）=λ1 f′（x3）（ x2-x1） …②
①×λ1+②×λ2，得
λ1 f （x1）+λ2 f （x2）-（λ1+λ2）f （x3）≥λ1λ2 f′（x3） （ x1-x2）+λ1λ2 f′（x3）（ x2-x1）=0
∴λ1 f （x1）+λ2 f （x2）≥（λ1+λ2）f （x3）=f （x3）=f（λ1 x1+λ2 x2）
猜想：λi＞0，xi＞0（i=1，2，…n）且λ1+λ2+…+λn=1时有
λ1 f （x1）+λ2 f （x2）+…+λn f （xn）≥f（λ1 x1+λ2 x2+…+λn xn）
（3）证明：令λi=
，xi=
，(i=1，2，…n)则有λ1+λ2+…+λn=1
由猜 想结论得：
lna1+
lna2+…+
lnan
≥-ln（
•
+
•
+…+
•
）
=-ln
=ln
∴a1lna1+a2lna2+…+anlnan≥（a1+a2+…+an） ln
即a1a1a2a2…anan≥(
)a1+a2+…+an
| 1 |
| x |
| 1-x |
| x2 |
当x∈（0，1）时F′（x）＞0，x∈（1，+∞）时F′（x）＜0
∴F（x）在（0，1）递增，在（1，+∞）递减，
∴当x=1时，函数有极大值为F（1）=0，
∴F（x）max=F（0）=0；∴当x＞0时，f （x）≤g（x） 恒成立，即 x＞0时 lnx≥1-
| 1 |
| x |
∴f （x2）-f （x1）=ln
| x1 |
| x2 |
| x2 |
| x1 |
| 1 |
| x1 |
（2）证明：设λ1＞0，λ2＞0且λ1+λ2=1
令x3=λ1 x1+λ2 x2，则x3＞0且x1-x3=λ2（x1-x2） x2-x3=λ1（x2-x1）
由（1）知f （x1）-f （x3）≥f′（x3）（ x1-x3）=λ2 f′（x3）（ x1-x2） …①
f （x2）-f （x3）≥f′（x3）（ x2-x3）=λ1 f′（x3）（ x2-x1） …②
①×λ1+②×λ2，得
λ1 f （x1）+λ2 f （x2）-（λ1+λ2）f （x3）≥λ1λ2 f′（x3） （ x1-x2）+λ1λ2 f′（x3）（ x2-x1）=0
∴λ1 f （x1）+λ2 f （x2）≥（λ1+λ2）f （x3）=f （x3）=f（λ1 x1+λ2 x2）
猜想：λi＞0，xi＞0（i=1，2，…n）且λ1+λ2+…+λn=1时有
λ1 f （x1）+λ2 f （x2）+…+λn f （xn）≥f（λ1 x1+λ2 x2+…+λn xn）
（3）证明：令λi=
| ai |
| a1+a2+…+an |
| 1 |
| ai |
由猜 想结论得：
| a1 |
| a1+a2+…+an |
| a2 |
| a1+a2+…+an |
| an |
| a1+a2+…+an |
≥-ln（
| a1 |
| a1+a2+…+an |
| 1 |
| a1 |
| a2 |
| a1+a2+…+an |
| 1 |
| a2 |
| an |
| a1+a2+…+an |
| 1 |
| an |
=-ln
| n |
| a1+a2+…+an |
| a1+a2+…+an |
| n |
∴a1lna1+a2lna2+…+anlnan≥（a1+a2+…+an） ln
| a1+a2+…+an |
| n |
即a1a1a2a2…anan≥(
| a1+a2+…+an |
| n |
点评：本题主要考查利用导数研究函数的极值问题及利用导数证明不等式成立问题，考查学生的问题的等价转化思想的运用能力及计算求解能力，逻辑性很强，属难题．
练习册系列答案
相关题目
已知x与y之间的一组数据为
则y与x的回归直线方程
=
x+
必过定点（ ）
| x | 1 | 2 | 3 | 4 |
| y | 1 | 5-a | 3 | 7+a |
 |
| y |
|
| b |
|
| a |
A、（4，
| ||
B、（
| ||
| C、（6，8） | ||
D、（
|
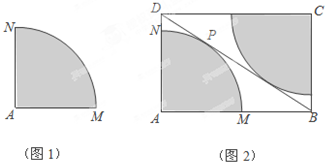某中学校园内原有一块四分之一圆面形状的草坪AMN（图1），其中AM=AN=8m，∠MAN=90°．今年暑假整治校园环境时，为美观起见，学校设计将原有草坪扩大，具体实施方案是：从圆弧上一点P作圆弧的切线BD，分别与AM，AN的延长线交于B，D，并以AB，AD为邻边构造矩形ABCD，再以C为圆心制作一块与AMN形状相同的草坪，构成矩形绿地ABCD（图2）．
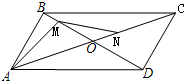如图，在平行四边形ABCD中，AD=2AB=2，∠BAD=60°，M、N分别是对角线BD、AC上的点，AC、BD相交于点O，已知BM=