题目内容
12.复数z=$\frac{(3+4i)^{2}}{(\sqrt{2}+i)^{4}(1-2i)^{2}}$,则|$\overline{z}$|=$\frac{5}{9}$.分析 利用|$\overline{z}$|=|z|及复数的模的性质及运算法则求解.
解答 解:∵z=$\frac{(3+4i)^{2}}{(\sqrt{2}+i)^{4}(1-2i)^{2}}$,
∴|$\overline{z}$|=|z|=$\frac{(\sqrt{9+16})^{2}}{(\sqrt{2+1})^{4}•(\sqrt{1+4})^{2}}$=$\frac{25}{9•5}$=$\frac{5}{9}$.
故答案为:$\frac{5}{9}$.
点评 本题考查复数的模的求法,是基础题,解题时要认真审题,注意复数的模的性质及运算法则的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
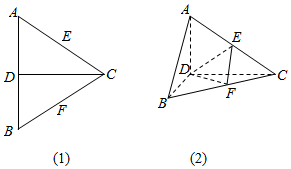 如图(1),正三角形ABC边长为2a,CD是AB边上的高,E,F分别为AC和BC边上的中点,现将△ABC沿CD翻折成直二面角A-DC-B(如图(2))
如图(1),正三角形ABC边长为2a,CD是AB边上的高,E,F分别为AC和BC边上的中点,现将△ABC沿CD翻折成直二面角A-DC-B(如图(2))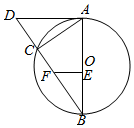 如图⊙O是Rt△ABC的外接圆,E、F是AB,BC上的点,且A,E,F,C四点共圆,延长BC至D,使得AC•BF=AD•BE.
如图⊙O是Rt△ABC的外接圆,E、F是AB,BC上的点,且A,E,F,C四点共圆,延长BC至D,使得AC•BF=AD•BE.