题目内容
17.已知函数f(x)=$\sqrt{1-{x}^{2}}$+$\sqrt{{x}^{2}-a}$是奇函数,求实数a满足的条件.分析 根据函数奇偶性的定义建立了方程关系进行求解即可.
解答 解:要使函数有意义,则$\left\{\begin{array}{l}{1-{x}^{2}≥0}\\{{x}^{2}-a≥0}\end{array}\right.$,
即$\left\{\begin{array}{l}{{x}^{2}≤1}\\{{x}^{2}≥a}\end{array}\right.$,
∵f(-x)=$\sqrt{1-{x}^{2}}$+$\sqrt{{x}^{2}-a}$=f(x),
∴若函数f(x)=$\sqrt{1-{x}^{2}}$+$\sqrt{{x}^{2}-a}$是奇函数,
则函数f(x)既是奇函数也是偶函数,
则f(x)=0,
即$\left\{\begin{array}{l}{1-{x}^{2}=0}\\{{x}^{2}-a=0}\end{array}\right.$则$\left\{\begin{array}{l}{{x}^{2}=1}\\{{x}^{2}=a}\end{array}\right.$,则a=1,
即要使函数f(x)是奇偶性,则a=1.
点评 本题主要考查函数奇偶性的应用和判断,利用函数奇偶性的定义建立方程关系是解决本题的关键.

练习册系列答案
相关题目
7.设a,b∈R,若p:a<b,q:$\frac{1}{b}$<$\frac{1}{a}$<0,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8.复数z=(2i-3)(1+2i)的实部与虚部之和为( )
| A. | -3 | B. | -11 | C. | 6 | D. | 4 |
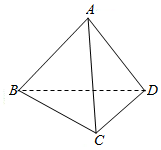 在空间四边形ABCD中,AB=AC=AD=1
在空间四边形ABCD中,AB=AC=AD=1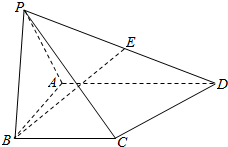 如图所示,在四棱锥P-ABCD中,△PAB为等边三角形,AD⊥AB,AD∥BC,平面PAB⊥平面ABCD,E为PD的中点.
如图所示,在四棱锥P-ABCD中,△PAB为等边三角形,AD⊥AB,AD∥BC,平面PAB⊥平面ABCD,E为PD的中点.