题目内容
5.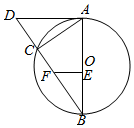 如图⊙O是Rt△ABC的外接圆,E、F是AB,BC上的点,且A,E,F,C四点共圆,延长BC至D,使得AC•BF=AD•BE.
如图⊙O是Rt△ABC的外接圆,E、F是AB,BC上的点,且A,E,F,C四点共圆,延长BC至D,使得AC•BF=AD•BE.(1)证明:DA是⊙O的切线;
(2)若AF•AB=1:$\sqrt{2}$,试求过点A、E、F、C的圆的面积与⊙O的面积之比.
分析 (1)证明:∠ACD=∠BEF,∠DAC=∠FBE,进而证明∠DAB=90°,即可证明DA是⊙O的切线;
(2)由(1)知AF为过A,E,F,C四点的圆的直径,利用AF:AB=1:$\sqrt{2}$,即可求过点A、E、F、C的圆的面积与⊙O的面积之比.
解答 (1)证明:由题意知∠ACD=90°,
∵A,E,F,C四点共圆,∴∠BEF=90°,即∠ACD=∠BEF.
又∵AC•BF=AD•BE,∴△ADC∽△BFE.
∴∠DAC=∠FBE.
∵∠FBE+∠BAC=90°,∴∠DAC+∠BAC=90°,
即∠DAB=90°,∴DA是⊙O的切线.…(5分)
(2)解:由(1)知AF为过A,E,F,C四点的圆的直径,
∵AF:AB=1:$\sqrt{2}$.∴AF2:AB2=1:2.
即过点A,E,F,C的圆的面积与⊙O的面积之比为1:2.…(10分)
点评 本题考查圆的切线的证明,考查四点共圆,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
15.已知函数f(x)=x(x-c)2在x=2处有极小值,则实数c的值为( )
| A. | 2 | B. | 2或6 | C. | 6 | D. | 4或6 |
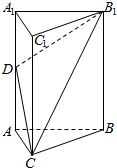 如图,三棱柱ABC-A1BC1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,D为A1A的中点.
如图,三棱柱ABC-A1BC1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,D为A1A的中点.