Question

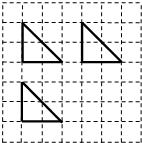如图，网格纸上的正方形小格的边长为l，图中的粗线画出了某几何体的三视图，则该几何体的表面积是（　　）

• A、4+2

  2

• B、4+4

  2

• C、6+2

  3

• D、6+3

  3

Answer 1

考点：由三视图求面积、体积

专题：空间位置关系与距离

分析：由已知中的三视图画出满足条件的几何体的直观图，进而求出各面的面积，相加可得答案．

解答： 解：由已知中的三视图，可得几何体的直观图如下所示：

其中PA⊥平面ABC，AB⊥BC，且PA=AB=BC=2，
故S_△PAB=S_△ABC=

1

2

×2×2=2，
S_△PAC=S_△PBC=

1

2

×2×2

2

=2

2

，
故该几何体的表面积是4+4

2

，
故选：B

点评：本题考查的知识点是由三视图求面积和体积，根据三视图判断几何体的形状是解答的关键．