题目内容
已知函数f(x)=sin(x+
),其中x∈[-
,a],若f(x)的值域是[-
,1],则实数a的取值范围是( )
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
A、(0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:先求得x+
的取值范围,由x+
∈[-
,
]时f(x)的值域是[-
,1],可知
≤a+
≤
,可解得实数a的取值范围.
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 6 |
| 7π |
| 6 |
解答:
解:∵x∈[-
,a],
∴x+
∈[-
,a+
],
∵x+
∈[-
,
]时f(x)的值域是[-
,1],
∴由函数的图象和性质可知
≤a+
≤
,可解得a∈[
,π].
故选:D.
| π |
| 3 |
∴x+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
∵x+
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| 1 |
| 2 |
∴由函数的图象和性质可知
| π |
| 2 |
| π |
| 6 |
| 7π |
| 6 |
| π |
| 3 |
故选:D.
点评:本题主要考察了正弦函数的图象和性质,由函数的图象和性质得到不等式
≤a+
≤
是解题的关键,属于基本知识的考查.
| π |
| 2 |
| π |
| 6 |
| 7π |
| 6 |

练习册系列答案
相关题目
在Rt△ABC中,CA=CB=3,M,N是斜边AB上的两个动点,且MN=
,则
•
的取值范围为( )
| 2 |
| CM |
| CN |
| A、[3,6] | ||
| B、[4,6] | ||
C、[2,
| ||
| D、[2,4] |
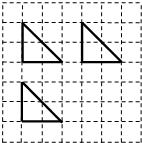 如图,网格纸上的正方形小格的边长为l,图中的粗线画出了某几何体的三视图,则该几何体的表面积是( )
如图,网格纸上的正方形小格的边长为l,图中的粗线画出了某几何体的三视图,则该几何体的表面积是( )A、4+2
| ||
B、4+4
| ||
C、6+2
| ||
D、6+3
|
设i是虚数单位,若复数m+
(m∈R)是纯虚数,则m的值为( )
| 10 |
| 3+i |
| A、-3 | B、-1 | C、1 | D、3 |
已知函数f(x)=
sin2x+cos2x,且-
≤x≤m+
+
-5(m>1)恒成立,则f(x)的值域为( )
| 3 |
| π |
| 6 |
| 4 |
| m-1 |
| π |
| 2 |
A、[
| ||
B、[1,
| ||
| C、[1,2] | ||
| D、[-1,2] |
程序框图如图所示,若其输出结果是140,则判断框中填写的是( )


| A、i<7 | B、i<8 |
| C、i>7 | D、i>8 |