题目内容
已知椭圆
+
=1(a>b>0),P(x,y),Q(x′,y′)是椭圆上两点,有下列三个不等式①a2+b2≥(x+y)2;②
+
≥(
+
)2③
+
≤1.其中不等式恒成立的序号是 .(填所有正确命题的序号)
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| x2 |
| 1 |
| y2 |
| 1 |
| a |
| 1 |
| b |
| xx′ |
| a2 |
| yy′ |
| b2 |
考点:命题的真假判断与应用
专题:圆锥曲线的定义、性质与方程
分析:依题意知,
+
=1,利用基本不等式及椭圆的有界性质对①②③三个不等式逐一分析判断即可.
| x2 |
| a2 |
| y2 |
| b2 |
解答:
解:由于 P(x,y)是椭圆
+
=1(a>b>0)上的点,则
+
=1,
故①(a2+b2)=(a2+b2)(
+
)=x2+y2+
y2+
x2≥(x+y)2,故①正确;
②(
+
)=(
+
)(
+
)≥(
+
)2,故②也正确;
③由于Q(x′,y′)是椭圆
+
=1(a>0,b>0)上的点.
令x=acosθ,y=bsinθ,x′=acosθ1,y′=bsinθ1,
则
=
=cosθcosθ1,
同理可得,
=sinθsinθ1,
∴
+
=cosθcosθ1+sinθsinθ1=cos(θ-θ1)≤1,故③也正确.
故答案为:①②③.
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
故①(a2+b2)=(a2+b2)(
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| b2 |
| b2 |
| a2 |
②(
| 1 |
| x2 |
| 1 |
| y2 |
| 1 |
| x2 |
| 1 |
| y2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| a |
| 1 |
| b |
③由于Q(x′,y′)是椭圆
| x2 |
| a2 |
| y2 |
| b2 |
令x=acosθ,y=bsinθ,x′=acosθ1,y′=bsinθ1,
则
| xx′ |
| a2 |
| acosθ•acosθ1 |
| a2 |
同理可得,
| yy′ |
| b2 |
∴
| xx′ |
| a2 |
| yy′ |
| b2 |
故答案为:①②③.
点评:本题考查命题的真假判断与应用,着重考查基本不等式及椭圆的有界性,考查等价转化思想与运算能力,属于中档题.

练习册系列答案
相关题目
设函数f(x)=ax2+b(a≠0),若∫
f(x)dx=2f(x0),x0>0,则x0=( )
2 0 |
| A、2 | ||||
B、
| ||||
| C、1 | ||||
D、
|
设
,
为单位向量.且
,
的夹角为
,若
=x
+(1-x)
,x∈[0,1],
=2
则向量
在
方向上的投影的取值范围是( )
| e1 |
| e2 |
| e1 |
| e2 |
| π |
| 3 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| a |
| b |
A、[
| ||
| B、[0,2] | ||
| C、[0,1] | ||
| D、[1,3] |
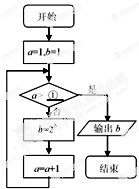 已知流程图如图(a=1,b=1下分别是a>①,b=2b,a=+1)所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填的是( )
已知流程图如图(a=1,b=1下分别是a>①,b=2b,a=+1)所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填的是( )