题目内容
7.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点(4,0),且其渐近线与圆(x-2)2+y2=3相切,则双曲线的方程为( )| A. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{8}$=1 | B. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 | D. | x2-$\frac{{y}^{2}}{16}$=1 |
分析 求出双曲线的渐近线方程,圆的圆心与半径,利用已知条件列出方程求解即可.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点(4,0),可得c=4,a2+b2=16,
双曲线的一条渐近线方程为:bx+ay=0,圆(x-2)2+y2=3的圆心(2,0),半径为$\sqrt{3}$.
渐近线与圆(x-2)2+y2=3相切,
可得:$\frac{|2b|}{\sqrt{{a}^{2}+{b}^{2}}}=\sqrt{3}$,
解得b=2$\sqrt{3}$,a=2,
所求的双曲线方程为:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1.
故选:C.
点评 本题考查圆的方程与双曲线方程的综合应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
15.已知正方体的不在同一表面的两个顶点A(-1,2,-1),B(3,-2,3),则正方体的棱长等于( )
| A. | 4 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
12.已知曲线x2+y2=2(x≥0,y≥0)和x+y=$\sqrt{2}$围成的封闭图形为Г,则图形Г绕y轴旋转一周后所形成几何体的表面积为( )
| A. | $\frac{2\sqrt{2}}{3}$ | B. | (8+4$\sqrt{2}$)π | C. | (8+2$\sqrt{2}$)π | D. | (4+2$\sqrt{2}$)π |
19.设f(x)是定义在(-π,0)∪(0,π)的奇函数,其导函数为f′(x),且$f({\frac{π}{2}})=0$,当x∈(0,π)时,f′(x)sinx-f(x)cosx<0,则关于x的不等式$f(x)<2f({\frac{π}{6}})sinx$的解集为( )
| A. | $({-\frac{π}{6},0})∪({0,\frac{π}{6}})$ | B. | $({-\frac{π}{6},0})∪({\frac{π}{6},π})$ | C. | $({-\frac{π}{6},0})∪({\frac{π}{6},\frac{π}{2}})$ | D. | $({-π,-\frac{π}{6}})∪({0,\frac{π}{6}})$ |
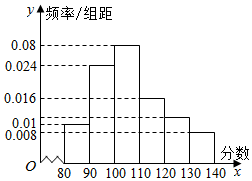 某校在2 015年11月份的高三期中考试后,随机地抽取了50名学生的数学成绩并进行了分析,结果这50名同学的成绩全部介于80分到140分之间.现将结果按如下方式分为6组,第一组[80,90),第二组[90,100),…第六组[130,140],得到如图所示的频率分布直方图.
某校在2 015年11月份的高三期中考试后,随机地抽取了50名学生的数学成绩并进行了分析,结果这50名同学的成绩全部介于80分到140分之间.现将结果按如下方式分为6组,第一组[80,90),第二组[90,100),…第六组[130,140],得到如图所示的频率分布直方图.