Question

2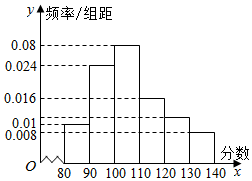．某校在2 015年11月份的高三期中考试后，随机地抽取了50名学生的数学成绩并进行了分析，结果这50名同学的成绩全部介于80分到140分之间．现将结果按如下方式分为6组，第一组[80，90），第二组[90，100），…第六组[130，140]，得到如图所示的频率分布直方图．
（Ⅰ）试估计该校数学的平均成绩（同一组中的数据用该区间的中点值作代表）；
（Ⅱ）这50名学生中成绩在120分以上的同学中任意抽取3人，该3人在130分（含130分）以上的人数记为X，求X的分布列和期望．

Answer 1

分析 （Ⅰ）根据频率分布直方图，求出成绩在[120，130）的频率以及平均成绩；
（Ⅱ）根据题意，计算对应的概率值，求出X的分布列与数学期望值．

解答 解：（Ⅰ）根据频率分布直方图，得：
成绩在[120，130）的频率为
1-（0.01×10+0.024×10+0.03×10+0.016×10+0.008×10）=1-0.88=0.12；
所以估计该校全体学生的数学平均成绩为
85×0.1+95×0.24+105×0.3+115×0.16+125×0.12+135×0.08=8.5+22.8+31.5+18.4+15+10.8=107，
所以该校的数学平均成绩为107；
（Ⅱ）根据频率分布直方图得，
这50人中成绩在130分以上（包括130分）的有0.08×50=4人，
而在[120，140]的学生共有0.12×50+0.08×50=10，
所以X的可能取值为0、1、2、3，
所以P（X=0）=$\frac{{C}_{6}^{3}}{{C}_{10}^{3}}$=$\frac{20}{120}$=$\frac{1}{6}$，P（X=1）=$\frac{{C}_{6}^{2}{•C}_{4}^{1}}{{C}_{10}^{3}}$=$\frac{60}{120}$=$\frac{1}{2}$，
P（X=2）=$\frac{{C}_{6}^{1}{•C}_{4}^{2}}{{C}_{10}^{3}}$=$\frac{36}{120}$=$\frac{3}{10}$，P（X=3）=$\frac{{C}_{4}^{3}}{{C}_{10}^{3}}$=$\frac{4}{120}$=$\frac{1}{30}$；
所以X的分布列为：

X	0	1	2	7
P	$\frac{1}{6}$	$\frac{1}{2}$	$\frac{3}{10}$	$\frac{1}{30}$

数学期望值为EX=0×$\frac{1}{6}$+1×$\frac{1}{2}$+2×$\frac{3}{10}$+3×$\frac{1}{30}$=1.2．

点评 本题考查了频率分布直方图的应用问题，也考查了离散型随机变量的分布列与数学期望的问题，是基础题目．