题目内容
已知sin(α+β)=
,0<α<
,-
<β<0,cosβ=
,则cosα= .
| 3 |
| 5 |
| π |
| 2 |
| π |
| 2 |
| 12 |
| 13 |
考点:两角和与差的余弦函数
专题:计算题,三角函数的求值
分析:由角的范围求出cos(α+β)、sinβ,再由cosα=cos[(α+β)-β],运用两角差的余弦公式,即可得到.
解答:
解:∵0<α<
,-
<β<0,
∴-
<α+β<
,
∵sin(α+β)=
,
∴cos(α+β)=
=
,
sinβ=-
=-
,
∴cosα=cos[(α+β)-β]=cos(α+β)cosβ+sin(α+β)sinβ
=
×
+
×(-
)=
.
故答案为:
.
| π |
| 2 |
| π |
| 2 |
∴-
| π |
| 2 |
| π |
| 2 |
∵sin(α+β)=
| 3 |
| 5 |
∴cos(α+β)=
1-(
|
| 4 |
| 5 |
sinβ=-
1-(
|
| 5 |
| 13 |
∴cosα=cos[(α+β)-β]=cos(α+β)cosβ+sin(α+β)sinβ
=
| 4 |
| 5 |
| 12 |
| 13 |
| 3 |
| 5 |
| 5 |
| 13 |
| 33 |
| 65 |
故答案为:
| 33 |
| 65 |
点评:本题考查三角函数的求值,考查两角差的余弦公式及运用,考查角的变换及运算能力,属于中档题.

练习册系列答案
 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
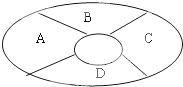 如图,A,B,C,D四个区域,现在有4种不同的颜色,给A,B,C,D四个区域涂色,要求每个区域只涂一色且相邻区域不涂同一色,则不同的涂法有
如图,A,B,C,D四个区域,现在有4种不同的颜色,给A,B,C,D四个区域涂色,要求每个区域只涂一色且相邻区域不涂同一色,则不同的涂法有