Question

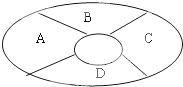如图，A，B，C，D四个区域，现在有4种不同的颜色，给A，B，C，D四个区域涂色，要求每个区域只涂一色且相邻区域不涂同一色，则不同的涂法有

 

种．

Answer 1

考点：计数原理的应用

专题：排列组合

分析：每个区域只涂一种颜色，相邻区域颜色不相同，然后分类研究，A、C不同色；A、C同色两大类．

解答： 解：分两种情况：
（1）A、C不同色（注意：B、D可同色、也可不同色，D只要不与A、C同色，所以D可以从剩余的2中颜色中任意取一色）：有4×3×2×2=48种；
（2）A、C同色（注意：B、D可同色、也可不同色，D只要不与A、C同色，所以D可以从剩余的3中颜色中任意取一色）：有4×3×1×3=36种．
共有84种
故答案为：84

点评：本题主要考查了分类计数原理，如何分类时关键．分类要全要细，属于中档题．