题目内容
13.已知向量$\overrightarrow{a}$=(t,1),$\overrightarrow{b}$=(2,t),若$\overrightarrow{a}$•$\overrightarrow{b}$=3,则|2$\overrightarrow{a}$+$\overrightarrow{b}$|=5.分析 根据数量积列出方程解出t,再求出2$\overrightarrow{a}+\overrightarrow{b}$的坐标,代入模长公式计算.
解答 解:∵$\overrightarrow{a}$•$\overrightarrow{b}$=2t+t=3,∴t=1.
∴$\overrightarrow{a}=(1,1)$,$\overrightarrow{b}=(2,1)$.
∴2$\overrightarrow{a}+\overrightarrow{b}$=(4,3),
∴|2$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{{4}^{2}+{3}^{2}}$=5.
故答案为:5.
点评 本题考查了平面向量数量积,模长的坐标运算,属于基础题.

练习册系列答案
相关题目
3.函数f(x)的导函数f′(x)的图象如图所示,则函数f(x)的解析式可能为( )
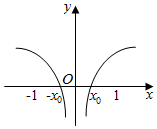

| A. | $\frac{{e}^{x}}{x}$ | B. | x2•lnx | C. | $\frac{{e}^{|x|}}{x}$ | D. | x•lnx2 |
4.某医院准备从6名骨科大夫中选派3名去农村三处医疗所做培训,要求甲、乙两位骨科组长至少有一人参加,那么不同的选派种数为( )
| A. | 96 | B. | 72 | C. | 60 | D. | 30 |
1.在数列{an}中,a1=$\frac{1}{2}$,a2=$\frac{1}{3}$,anan+2=1,则a2016+a2017=( )
| A. | $\frac{5}{6}$ | B. | $\frac{7}{3}$ | C. | $\frac{7}{2}$ | D. | 5 |
8.定义在(0,π)上的函数y=f(x)满足f′(x)<f(x)•cotx,则下列不等式错误的是( )
| A. | sin1•f($\frac{1}{2}$)>sin$\frac{1}{2}$•f(1) | B. | $\frac{1}{2}$•f($\frac{1}{2}$)>sin$\frac{1}{2}$•f($\frac{π}{6}$) | ||
| C. | sin2•f(1)>sin1•f(2) | D. | f($\frac{π}{3}$)>$\sqrt{3}$f($\frac{π}{6}$) |