题目内容
17.函数$y={log_{\frac{1}{2}}}({-{x^2}+2x})的$的单调增区间是[1,2).分析 先求出函数的定义域,结合二次函数,对数函数和复合函数的单调性,可得答案.
解答 解:由-x2+2x>0得:x∈(0,2),
故函数$y=lo{g}_{\frac{1}{2}}(-{x}^{2}+2x)$的定义域为(0,2),
由t=-x2+2x在[1,2)上为减函数,y=${log}_{\frac{1}{2}}t$为减函数,
故函数$y=lo{g}_{\frac{1}{2}}(-{x}^{2}+2x)$的单调递增区间为[1,2),
故答案为:[1,2).
点评 本题考查的知识点是对数函数的图象和性质,熟练掌握对数函数的图象和性质,是解答的关键.

练习册系列答案
相关题目
5.△ABC中,$AB=\sqrt{2}$,BC=2,$sinA=\frac{{\sqrt{14}}}{4}$,则sinC=( )
| A. | $\frac{{\sqrt{3}}}{4}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{7}}}{4}$ | D. | $\frac{{\sqrt{7}}}{3}$ |
9.已知集合 A={x|-2≤x≤3},B={x|x<-1},则集合A∩B=( )
| A. | {x|-2≤x<4} | B. | {x|x≤3或x≥4} | C. | {x|-2≤x<-1} | D. | {x|-1≤x≤3} |
7.若{an}为等比数列,则“a1<a3<a5”是“数列{an}是递增数列”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
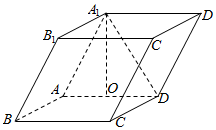 如图,四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,且AD=2CD=2,AA1=2,$∠{A_1}AD=\frac{π}{3}$,若O为AD的中点,且CD⊥A1O.
如图,四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,且AD=2CD=2,AA1=2,$∠{A_1}AD=\frac{π}{3}$,若O为AD的中点,且CD⊥A1O.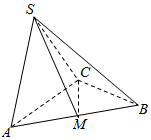 如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,SA=SC=SA=SC,M为AB的中点.
如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,SA=SC=SA=SC,M为AB的中点.