题目内容

5．求下列函数的反函数：
（1）y=4x-2；
（2）y=$\frac{2}{x}$+3．

分析 由已知解析式，用y表示出x，然后把x与y互换，即得反函数，应注意定义域与值域的互换．

解答 解：（1）∵y=4x-2，化为x=$\frac{1}{4}$y+$\frac{1}{2}$，把x与y互换可得：y=$\frac{1}{4}$x+$\frac{1}{2}$，（x∈R）；
（2）∵y=$\frac{2}{x}$+3（x≠0），化为x=$\frac{2}{y-3}$，把x与y互换可得：y=$\frac{2}{x-3}$，（x≠3）．

点评 本题考查了反函数的定义与求法问题，是基础题目．

练习册系列答案
相关题目
15．设数列{an}的前n项和为Sn，对任意正整数n，3an-2Sn=2．
（I）求数列{an}的通项公式；
（Ⅱ）求证：Sn+2Sn＜${S}_{n+1}^{2}$．
16．数列{an}中a1=2，an+1=（$\sqrt{2}$-1）（an+2），n∈N*，则{an}的通项公式为${a}_{n}=\sqrt{2}（\sqrt{2}-1）^{n}+\sqrt{2}$．
变式：已知数列{an}中a1=2，an+1=2an3，n∈N*，则{an}的通项公式为${a}_{n}={2}^{\frac{1}{2}（{3}^{n}-1）}$．
13．已知向量$\overrightarrow{a}$=（t，1），$\overrightarrow{b}$=（2，t），若$\overrightarrow{a}$•$\overrightarrow{b}$=3，则|2$\overrightarrow{a}$+$\overrightarrow{b}$|=5．
20．已知A（-1，0）、B（2，1）、C（5，-8），△ABC的外接圆在点A处的切线为l，则点B到直线l的距离为1．
4．设函数f（x）=（x+a）lnx-x+a．
（1）设g（x）=f′（x），求函数g（x）的单调区间；
（2）已知?a＞0，?0＜x＜a，使得a+xlnx＞0，试研究a＞0时函数y=f（x）的零点个数．
11．设点A1，A2分别为椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左右顶点，若在椭圆C上存在异于点A1，A2的点P，使得PO⊥PA2，其中O为坐标原点，则椭圆C的离心率的取值范围是（$\frac{\sqrt{2}}{2}$，1）．
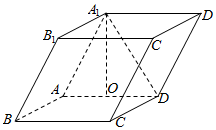8．如图，四棱柱ABCD-A1B1C1D1中，底面ABCD是矩形，且AD=2CD=2，AA1=2，$∠{A_1}AD=\frac{π}{3}$，若O为AD的中点，且CD⊥A1O．
（Ⅰ）求证：A1O⊥平面ABCD；
（Ⅱ）线段BC上是否存在一点P，使得二面角D-A1A-P的大小为$\frac{π}{3}$？若存在，求出BP的长；若不存在，说明理由．
9．已知集合 A={x|-2≤x≤3}，B={x|x＜-1}，则集合A∩B=（　　）
A．{x|-2≤x＜4}B．{x|x≤3或x≥4}C．{x|-2≤x＜-1}D．{x|-1≤x≤3}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网