题目内容
8.定义在(0,π)上的函数y=f(x)满足f′(x)<f(x)•cotx,则下列不等式错误的是( )| A. | sin1•f($\frac{1}{2}$)>sin$\frac{1}{2}$•f(1) | B. | $\frac{1}{2}$•f($\frac{1}{2}$)>sin$\frac{1}{2}$•f($\frac{π}{6}$) | ||
| C. | sin2•f(1)>sin1•f(2) | D. | f($\frac{π}{3}$)>$\sqrt{3}$f($\frac{π}{6}$) |
分析 构造函数g(x)=$\frac{f(x)}{sinx}$,求出g(x)的单调性,从而判断函数值的大小即可.
解答 解:令g(x)=$\frac{f(x)}{sinx}$,则g′(x)=$\frac{f′(x)sinx-f(x)cosx}{{sin}^{2}x}$,
由f′(x)<f(x)•cotx得:f′(x)sinx-f(x)cosx<0,
∴g′(x)<0在(0,π)恒成立,g(x)在(0,π)递减,
∴g($\frac{1}{2}$)>g(1),A正确,g($\frac{1}{2}$)>g($\frac{π}{6}$),B正确,
g(1)>g(2),C正确,g($\frac{π}{3}$)<g($\frac{π}{6}$),D错误,
故选:D.
点评 本题考查了函数的单调性问题,考查导数的应用,构造函数g(x)=$\frac{f(x)}{sinx}$,求出g(x)的单调性是解题的关键,本题是一道中档题.

练习册系列答案
相关题目

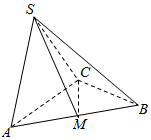 如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,SA=SC=SA=SC,M为AB的中点.
如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,SA=SC=SA=SC,M为AB的中点.