题目内容
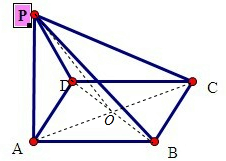
 如图,已知四棱锥P-ABCD中,PA⊥底面ABCD,底面是正方形ABCD,PA=AB=2.
如图,已知四棱锥P-ABCD中,PA⊥底面ABCD,底面是正方形ABCD,PA=AB=2.(1)求二面P-BD-A角的余弦值;
(2)求四棱锥P-ABCD的外接球的表面积.
考点:棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离,空间角
分析:(1)连接AC,BD,AC∩BD=O,连接PO,则∠AOP是二面P-BD-A角的平面角,可求二面P-BD-A角的余弦值;
(2)四棱锥P-ABCD可补成正方体,其对角线长为2
,是四棱锥P-ABCD的外接球的直径,即可求四棱锥P-ABCD的外接球的表面积.
(2)四棱锥P-ABCD可补成正方体,其对角线长为2
| 3 |
解答:
 解:(1)连接AC,BD,AC∩BD=O,则AO⊥BD,
解:(1)连接AC,BD,AC∩BD=O,则AO⊥BD,
连接PO,则PO⊥BD,
∴∠AOP是二面P-BD-A角的平面角,
∵PA-2,OA=
,
∴PO=
,
∴cos∠AOP=
∴二面P-BD-A角的余弦值为
;
(2)四棱锥P-ABCD可补成正方体,其对角线长为2
,
∴四棱锥P-ABCD的外接球的直径为2
,
∴四棱锥P-ABCD的外接球的表面积为4π•(
)2=12π.
 解:(1)连接AC,BD,AC∩BD=O,则AO⊥BD,
解:(1)连接AC,BD,AC∩BD=O,则AO⊥BD,连接PO,则PO⊥BD,
∴∠AOP是二面P-BD-A角的平面角,
∵PA-2,OA=
| 2 |
∴PO=
| 6 |
∴cos∠AOP=
| ||
|
∴二面P-BD-A角的余弦值为
| ||
| 3 |
(2)四棱锥P-ABCD可补成正方体,其对角线长为2
| 3 |
∴四棱锥P-ABCD的外接球的直径为2
| 3 |
∴四棱锥P-ABCD的外接球的表面积为4π•(
| 3 |
点评:本题考查四棱锥P-ABCD的外接球的表面积,考查面面角,考查学生分析解决问题的能力,属于中档题.解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
函数f(x)=2sinxcosx的最小值是( )
| A、-1 | B、-2 | C、2 | D、1 |
若直线l1,l2的方向向量分别为
=(2,4,-4),
=(-6,9,6),则( )
| a |
| b |
| A、l1∥l2 |
| B、l1⊥l2 |
| C、l1与l2相交但不垂直 |
| D、以上均不正确 |