题目内容
已知向量
=
,
,
=
,
,设函数f(x)=
•
.
(Ⅰ)求f(x)的单调递增区间;
(Ⅱ)在△ABC中,a、b、c分别是角A、B、C的对边,若2
•
=
ab,c=2
,f(A)=4,求b.
| m |
|
|
| n |
|
|
| m |
| n |
(Ⅰ)求f(x)的单调递增区间;
(Ⅱ)在△ABC中,a、b、c分别是角A、B、C的对边,若2
| AC |
| BC |
| 2 |
| 2 |
考点:正弦定理的应用,平面向量的综合题
专题:计算题,三角函数的图像与性质,平面向量及应用
分析:(Ⅰ)运用平面向量的数量积的坐标公式,及两角和的正弦公式,以及正弦函数的增区间,即可得到所求;
(Ⅱ)由向量的数量积的定义,求得C,再由f(A)=4,求得A,再由正弦定理,即可得到b.
(Ⅱ)由向量的数量积的定义,求得C,再由f(A)=4,求得A,再由正弦定理,即可得到b.
解答:
解:(Ⅰ)∵
=
,
,
=
,
∴f(x)=
•
=
sin2x+cos2x+3
=2sin(2x+
)+3,
令2kπ-
≤2x+
≤2kπ+
,
故kπ-
≤x≤kπ+
(k∈Z),
则f(x)的单调递增区间为[kπ-
,kπ+
](k∈Z).
(Ⅱ)∵2
•
=
ab,∴2bacosC=
ab,cosC=
,
∵0<C<π,∴C=
,
由f(A)=4得f(A)=2sin(2A+
)+3=4,
∴sin(2A+
)=
,
又A为△ABC的内角,
<2A+
<
,2A+
=
,∴A=
,
由于c=2
,由正弦定理,得
=
⇒
=
⇒b=4sin(
+
),
则b=4(
+
)=
+
.
| m |
|
|
| n |
|
|
∴f(x)=
| m |
| n |
| 3 |
=2sin(2x+
| π |
| 6 |
令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
故kπ-
| π |
| 3 |
| π |
| 6 |
则f(x)的单调递增区间为[kπ-
| π |
| 3 |
| π |
| 6 |
(Ⅱ)∵2
| AC |
| BC |
| 2 |
| 2 |
| ||
| 2 |
∵0<C<π,∴C=
| π |
| 4 |
由f(A)=4得f(A)=2sin(2A+
| π |
| 6 |
∴sin(2A+
| π |
| 6 |
| 1 |
| 2 |
又A为△ABC的内角,
| π |
| 6 |
| π |
| 6 |
| 13π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 3 |
由于c=2
| 2 |
| b |
| sinB |
| c |
| sinC |
| b |
| sin(π-A-C) |
2
| ||||
|
| π |
| 4 |
| π |
| 3 |
则b=4(
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| 6 |
点评:本题考查平面向量的数量积的坐标公式和三角函数的恒等变换公式的运用,同时考查正弦函数的单调性,以及正弦定理的运用,考查两角和差公式,以及运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
抛物线y2=-16x的焦点坐标为( )
| A、(0,-4) |
| B、(4,0) |
| C、(0,4) |
| D、(-4,0) |
函数f(x)=x3-3x2-9x+3,若函数g(x)=f(x)-m,在x∈[-2,5]上有3个零点,则m的取值范围为( )
| A、[1,8] |
| B、(-24,1] |
| C、[1,8) |
| D、(-24,8) |
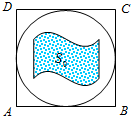 如图,在边长为2的正方形ABCD中有一内切圆,某人为了用随机模拟的方法估计出该圆内阴影部分(旗帜)的面积S0,往正方形ABCD内随机撒了100粒品质相同 的豆子,结果有75粒落在圆内,有25粒落在阴影部分内,据此,有五种说法:
如图,在边长为2的正方形ABCD中有一内切圆,某人为了用随机模拟的方法估计出该圆内阴影部分(旗帜)的面积S0,往正方形ABCD内随机撒了100粒品质相同 的豆子,结果有75粒落在圆内,有25粒落在阴影部分内,据此,有五种说法: