题目内容
已知命题p:对任意的区间[1,2]内的实数x,x2-a≥0恒成立;命题q:方程x2+2ax+2-a=0有实根.若命题p,q都是真命题,求实数a的取值范围.
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:令f(x)=x2,利用等价转化思想可知a≤f(x)min,易求f(x)min=1,从而可求命题p为真命题时a的取值范围;同理可求得命题q是真命题时a的取值范围,利用p∧q为真,即可求得答案.
解答:
解:命题p:∵?x∈[1,2],x2-a≥0恒成立,令f(x)=x2,
则a≤f(x)min;
∵f(x)=x2在区间[1,2]上单调递增,
∴f(x)min=f(1)=1,
∴a≤1;
命题q:∵方程x2+2ax+2-a=0有实根,
∴△=(2a)2-4×1×(2-a)≥0,
整理得:a2+a-2≥0,
解得:a≥1或a≤-2;
∵命题p,q都是真命题,
∴a=1或a≤-2;
即实数a的取值范围为{a|a=1或a≤-2}.
则a≤f(x)min;
∵f(x)=x2在区间[1,2]上单调递增,
∴f(x)min=f(1)=1,
∴a≤1;
命题q:∵方程x2+2ax+2-a=0有实根,
∴△=(2a)2-4×1×(2-a)≥0,
整理得:a2+a-2≥0,
解得:a≥1或a≤-2;
∵命题p,q都是真命题,
∴a=1或a≤-2;
即实数a的取值范围为{a|a=1或a≤-2}.
点评:本题考查命题的真假判断与应用,考查函数恒成立问题,突出等价转化思想与运算求解能力的考查,属于中档题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
已知△ABC是正三角形,且它的边长为a,那么它的直观图△A′B′C′的面积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知集合A={0,1,2},B={x-y|x∈A,y∈A},则集合B中元素的个数为( )
| A、3 | B、5 | C、7 | D、9 |
已知双曲线C1:
-
=1(a>0,b>0)的焦距是实轴长的2倍.若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、x2=
| ||||
B、x2=
| ||||
| C、x2=8y | ||||
| D、x2=16y |
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为H.则以下命题中,错误的命题是( )
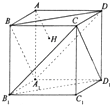

| A、点H是△A1BD的垂心 |
| B、AH垂直平面CB1D1 |
| C、直线AH和BB1所成角为45° |
| D、AH的延长线经过点C1 |
 如图,在四棱锥P-ABCD中,AB∥CD,△PAB和△PAD是两个边长为2的正三角形.DC=4,PD⊥PB,点E是CD的中点.
如图,在四棱锥P-ABCD中,AB∥CD,△PAB和△PAD是两个边长为2的正三角形.DC=4,PD⊥PB,点E是CD的中点. 已知ABCD-A1B1C1D1是边长为3的正方体,点P、Q、R分别是棱AB、AD、AA1上的点,AP=AQ=AR=1,则四面体C1PQR的体积为
已知ABCD-A1B1C1D1是边长为3的正方体,点P、Q、R分别是棱AB、AD、AA1上的点,AP=AQ=AR=1,则四面体C1PQR的体积为