题目内容
已知集合M、N,在①M∩N⊆N,②M∪N⊆N,③M∩N⊆M∪N,④若M⊆N,则M∩N=M中,正确的个数有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:集合的包含关系判断及应用
专题:计算题,集合
分析:利用M∩N中的元素是集合M和集合N的公共元素,M∪N中的元素是集合A和集合B的所有元素这些知识对所给的选项逐个判断,能够得到答案.
解答:
解:∵M∩N中的元素是集合M和集合N的公共元素,
∴(M∩N)⊆N,故①成立;
∵M∪N中的元素是集合M和集合N的所有元素,
∴②不成立;
∵M∩N中的元素是集合M和集合N的公共元素,
M∪N中的元素是集合A和集合B的所有元素,
∴(M∩N)⊆(M∪N),故③成立;
若M⊆N,则M∩N=M,故④成立.
故选C.
∴(M∩N)⊆N,故①成立;
∵M∪N中的元素是集合M和集合N的所有元素,
∴②不成立;
∵M∩N中的元素是集合M和集合N的公共元素,
M∪N中的元素是集合A和集合B的所有元素,
∴(M∩N)⊆(M∪N),故③成立;
若M⊆N,则M∩N=M,故④成立.
故选C.
点评:本题考查集合的交、并、补集的运算,解题时要认真审题,熟练掌握集合的运算法则和集合间的相互关系.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
函数y=f(x)在定义域内可导,若f(x)关于点(1,0)对称,且当x<(-∞,1)时,f′(x)<0,设a=f(0),b=f(
),c=f(3),将a,b,c按从小到大用“<”连接起来,结果为 .
| 1 |
| 2 |
斜率不存在的直线一定是( )
| A、平行于x轴的直线 |
| B、垂直于x轴的直线 |
| C、垂直于y轴的直线 |
| D、垂直于坐标轴的直线 |
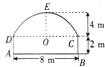 如图所示的图形为一隧道的截面,其中ABCD是矩形,CED是抛物线的一段,在工程的设计中,要注意开凿隧道所需挖掘的土石方量,这就需要计算这个截面的面积,试根据图中所给出的数据计算这个截面的面积.
如图所示的图形为一隧道的截面,其中ABCD是矩形,CED是抛物线的一段,在工程的设计中,要注意开凿隧道所需挖掘的土石方量,这就需要计算这个截面的面积,试根据图中所给出的数据计算这个截面的面积.